题目内容
20.有甲、乙两位同学,根据“关于x的一元二次方程kx2-(k+2)x+2=0”(k为实数)这一已知条件,他们各自提出了一个问题考查对方,问题如下:甲:你能不解方程判断方程实数根的情况吗?
乙:若方程有两个不相等的正整数根,你知道整数k的值等于多少吗?请你帮助两人解决上述问题.
分析 (1)首先根据一元二次方程的定义得出k≠0,再计算△=(k+2)2-4k×2=(k-2)2≥0,由判别式的意义即可判定方程有实数根;
(2)利用因式分解法求出方程的两根为x1=1,x2=$\frac{2}{k}$,根据方程有两个不相等的正整数根,得出整数k=1.
解答 解:(1)∵kx2-(k+2)x+2=0(k为实数)是关于x的一元二次方程,
∴k≠0,
∵△=(k+2)2-4k×2=(k-2)2≥0,
∴方程有实数根;
(2)kx2-(k+2)x+2=0,
(x-1)(kx-2)=0,
x-1=0,或kx-2=0,
解得x1=1,x2=$\frac{2}{k}$,
∵方程有两个不相等的正整数根,且k为整数,
∴k=1或2,
∵k=2时,x1=x2=1,两根相等,不合题意舍去,
∴k=1.
点评 本题考查了根的判别式,一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac有如下关系:
①当△>0时,方程有两个不相等的两个实数根;
②当△=0时,方程有两个相等的两个实数根;
③当△<0时,方程无实数根.
也考查了因式分解法解一元二次方程.

练习册系列答案
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
5.若am=2,an=3,则a3m-2n等于( )
| A. | 5 | B. | -1 | C. | $\frac{8}{9}$ | D. | 9 |
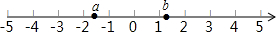 已知:实数a,b在数轴上的位置如图所示,化简:$\sqrt{(a+1)^{2}}$+2$\sqrt{(b-1)^{2}}$-|a-b|.
已知:实数a,b在数轴上的位置如图所示,化简:$\sqrt{(a+1)^{2}}$+2$\sqrt{(b-1)^{2}}$-|a-b|.
 已知一次函数y=kx+b的图象平行于直线y=-3x,且经过点(2,-3).
已知一次函数y=kx+b的图象平行于直线y=-3x,且经过点(2,-3).