题目内容
9.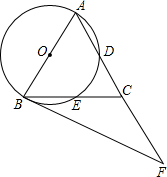 如图,在△ABC中,AB=AC,∠BAC=54°,以AB为直径的⊙O分别交AC,BC于点D、E,过点B作⊙O的切线,交AC的延长线于点F.
如图,在△ABC中,AB=AC,∠BAC=54°,以AB为直径的⊙O分别交AC,BC于点D、E,过点B作⊙O的切线,交AC的延长线于点F.(1)求证:BE=CE;
(2)求∠CBF的度数;
(3)若AB=5,求$\widehat{AD}$的长.
分析 (1)连接AE,求出AE⊥BC,根据等腰三角形性质求出即可;
(2)求出∠ABC,求出∠ABF,即可求出答案;
(3)求出∠AOD度数,求出半径,即可求出答案.
解答 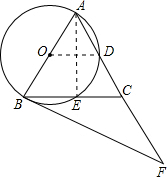 (1)证明:连接AE,
(1)证明:连接AE,
∵AB是⊙O直径,
∴∠AEB=90°,
即AE⊥BC,
∵AB=AC,
∴BE=CE.
(2)解:∵∠BAC=54°,AB=AC,
∴∠ABC=63°,
∵BF是⊙O切线,
∴∠ABF=90°,
∴∠CBF=∠ABF-∠ABC=27°.
(3)解:连接OD,
∵OA=OD,∠BAC=54°,
∴∠AOD=72°,
∵AB=5,
∴OA=2.5,
∴弧AD的长是$\frac{72π×2.5}{180}$=π.
点评 本题考查了切线的性质,等腰三角形的性质,弧长公式,圆周角定理的应用,主要考查学生运用定理进行推理和计算的能力.

练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案
相关题目
14.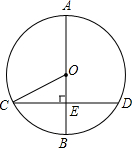 如图,⊙O的直径AB长为10,弦CD的长为8,CD⊥AB于点E,则tan∠OCE=( )
如图,⊙O的直径AB长为10,弦CD的长为8,CD⊥AB于点E,则tan∠OCE=( )
 如图,⊙O的直径AB长为10,弦CD的长为8,CD⊥AB于点E,则tan∠OCE=( )
如图,⊙O的直径AB长为10,弦CD的长为8,CD⊥AB于点E,则tan∠OCE=( )| A. | $\frac{3}{4}$ | B. | $\frac{3}{5}$ | C. | $\frac{4}{3}$ | D. | $\frac{4}{5}$ |
 如图,在?ABCD中,E为CD中点,AE与BD相交于点O,S△DOE=3cm2,则S△ADB等于18cm2.
如图,在?ABCD中,E为CD中点,AE与BD相交于点O,S△DOE=3cm2,则S△ADB等于18cm2.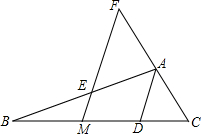 已知在△ABC中,AD平分∠BAC,MF∥AD交AB于点E,交BC于点M,求证:$\frac{BE}{CF}=\frac{BM}{CM}$.
已知在△ABC中,AD平分∠BAC,MF∥AD交AB于点E,交BC于点M,求证:$\frac{BE}{CF}=\frac{BM}{CM}$.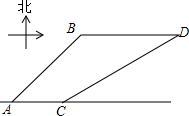 如图,港口B在港口A的东北方向,相距40$\sqrt{2}$海里,上午9时,一艘轮船从港口A出发,以15海里/时的速度向正东方向航行,同时一艘快艇从港口B出发也向正东方向航行,上午11时轮船到达C处,同时快艇到达D处,测试测得D在C的北偏东60°方向上,求快艇每小时航行多少海里?
如图,港口B在港口A的东北方向,相距40$\sqrt{2}$海里,上午9时,一艘轮船从港口A出发,以15海里/时的速度向正东方向航行,同时一艘快艇从港口B出发也向正东方向航行,上午11时轮船到达C处,同时快艇到达D处,测试测得D在C的北偏东60°方向上,求快艇每小时航行多少海里?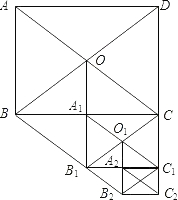 如图,在矩形ABCD中,AB=6,BC=10,两条对角线相交于点O,以OB,OC为邻边作第1个平行四边形OBB1C,对角线相交于点A1,再以A1B1、A1C为邻边作第2个平行四边形A1B1C1C,对角线相交于点O1;再以O1B1、O1C1为邻边作第3个平行四边形O1B1B2C1…依此类推.则第6个平行四边形的面积是$\frac{15}{16}$.
如图,在矩形ABCD中,AB=6,BC=10,两条对角线相交于点O,以OB,OC为邻边作第1个平行四边形OBB1C,对角线相交于点A1,再以A1B1、A1C为邻边作第2个平行四边形A1B1C1C,对角线相交于点O1;再以O1B1、O1C1为邻边作第3个平行四边形O1B1B2C1…依此类推.则第6个平行四边形的面积是$\frac{15}{16}$.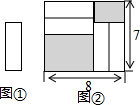 把四张形状大小完全相同的小长方形卡片(如图①)不重叠地放在一个底面长为8,宽为7的长方形盒子底部(如图②),盒子底面未被卡片覆盖的部分用阴影表示,则图②中两块阴影部分周长和是30.
把四张形状大小完全相同的小长方形卡片(如图①)不重叠地放在一个底面长为8,宽为7的长方形盒子底部(如图②),盒子底面未被卡片覆盖的部分用阴影表示,则图②中两块阴影部分周长和是30.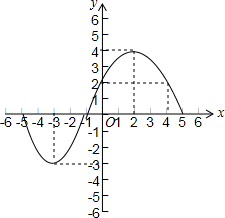 观察图,解答下列问题:
观察图,解答下列问题: