题目内容
1.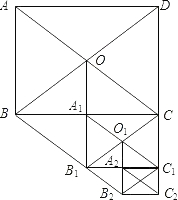 如图,在矩形ABCD中,AB=6,BC=10,两条对角线相交于点O,以OB,OC为邻边作第1个平行四边形OBB1C,对角线相交于点A1,再以A1B1、A1C为邻边作第2个平行四边形A1B1C1C,对角线相交于点O1;再以O1B1、O1C1为邻边作第3个平行四边形O1B1B2C1…依此类推.则第6个平行四边形的面积是$\frac{15}{16}$.
如图,在矩形ABCD中,AB=6,BC=10,两条对角线相交于点O,以OB,OC为邻边作第1个平行四边形OBB1C,对角线相交于点A1,再以A1B1、A1C为邻边作第2个平行四边形A1B1C1C,对角线相交于点O1;再以O1B1、O1C1为邻边作第3个平行四边形O1B1B2C1…依此类推.则第6个平行四边形的面积是$\frac{15}{16}$.
分析 首先分别求得几个平行四边形的面积,即可得到规律:第n个平行四边形的面积为:$\frac{60}{{2}^{n}}$,继而求得答案.
解答 解:∵在矩形ABCD中,AB=6,BC=10,
∴S矩形ABCD=AB•CD=60,OB=OC,
∵以OB,OC为邻边作第1个平行四边形OBB1C,
∴平行四边形OBB1C是菱形,
∴S?OBB1C=$\frac{1}{2}$BC•OB1=$\frac{1}{2}$×10×6=30,
S?A1B1C1C=A1C•A1B1=15,
∴第n个平行四边形的面积为:$\frac{60}{{2}^{n}}$,
∴第6个平行四边形的面积是:$\frac{60}{{2}^{6}}$=$\frac{15}{16}$.
故答案为:$\frac{15}{16}$.
点评 此题考查了平行四边形的性质以及矩形的性质.注意得到规律:第n个平行四边形的面积为$\frac{60}{{2}^{n}}$是关键.

练习册系列答案
相关题目
12.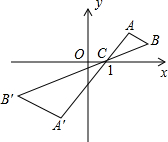 如图,△ABC中,A、B两个顶点在x轴的上方,点C的坐标是(1,0),以点C位似中心,在x轴的下方作△ABC的位似图形△A′B′C,并把△ABC的边长放大到原来的2倍,设点B的横坐标是a,则点B的对应点B′的横坐标是( )
如图,△ABC中,A、B两个顶点在x轴的上方,点C的坐标是(1,0),以点C位似中心,在x轴的下方作△ABC的位似图形△A′B′C,并把△ABC的边长放大到原来的2倍,设点B的横坐标是a,则点B的对应点B′的横坐标是( )
 如图,△ABC中,A、B两个顶点在x轴的上方,点C的坐标是(1,0),以点C位似中心,在x轴的下方作△ABC的位似图形△A′B′C,并把△ABC的边长放大到原来的2倍,设点B的横坐标是a,则点B的对应点B′的横坐标是( )
如图,△ABC中,A、B两个顶点在x轴的上方,点C的坐标是(1,0),以点C位似中心,在x轴的下方作△ABC的位似图形△A′B′C,并把△ABC的边长放大到原来的2倍,设点B的横坐标是a,则点B的对应点B′的横坐标是( )| A. | -2a | B. | 2a-2 | C. | 3-2a | D. | 2a-3 |
6.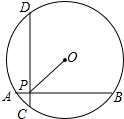 如图,在半径为10的⊙O中,AB,CD是互相垂直的两条弦,垂足为P,且AB=CD=16,则OP的长为( )
如图,在半径为10的⊙O中,AB,CD是互相垂直的两条弦,垂足为P,且AB=CD=16,则OP的长为( )
 如图,在半径为10的⊙O中,AB,CD是互相垂直的两条弦,垂足为P,且AB=CD=16,则OP的长为( )
如图,在半径为10的⊙O中,AB,CD是互相垂直的两条弦,垂足为P,且AB=CD=16,则OP的长为( )| A. | 6 | B. | 6$\sqrt{2}$ | C. | 8 | D. | 8$\sqrt{2}$ |
13. 如图,已知:∠1=∠2,∠D=50°,则∠B的度数是( )
如图,已知:∠1=∠2,∠D=50°,则∠B的度数是( )
 如图,已知:∠1=∠2,∠D=50°,则∠B的度数是( )
如图,已知:∠1=∠2,∠D=50°,则∠B的度数是( )| A. | 50° | B. | 130° | ||
| C. | 150° | D. | 以上结果均不正确 |
10.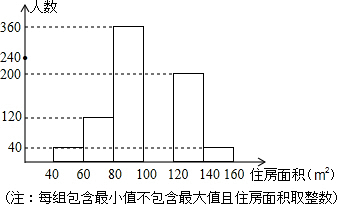 2013年合肥市春季房交会期间,某公司对参加本次房交会的消费者进行了随即问卷调查,共发放1000份调查问卷,并全部收回.根据调查问卷,将消费者年收入的情况整理后,制成表格如下:
2013年合肥市春季房交会期间,某公司对参加本次房交会的消费者进行了随即问卷调查,共发放1000份调查问卷,并全部收回.根据调查问卷,将消费者年收入的情况整理后,制成表格如下:
将消费者打算购买住房面积的情况整理后,作出部分频数分布直方图.
注:每组包含最小值不包含最大值,且住房面积取整数.
请你根据以上信息,回答下列问题:
(1)根据表格可得,被调查的消费者平均年收入为2.39万元;被调查的消费者中年收入的中位数是1.8;在平均数与中位数这两个数中,中位数更能反映被调查的消费者年收入的一般水平.
(2)根据频数分布直方图可得,打算购买100-120m2房子的人数为240人;打算购买住房面积小于100m2的消费者占被调查消费者人数的百分数是52%.
(3)在图中补全这个频数分布直方图.
 2013年合肥市春季房交会期间,某公司对参加本次房交会的消费者进行了随即问卷调查,共发放1000份调查问卷,并全部收回.根据调查问卷,将消费者年收入的情况整理后,制成表格如下:
2013年合肥市春季房交会期间,某公司对参加本次房交会的消费者进行了随即问卷调查,共发放1000份调查问卷,并全部收回.根据调查问卷,将消费者年收入的情况整理后,制成表格如下:| 年收入(万元) | 3.2 | 3.8 | 5.0 | 7.0 | 12.0 |
| 被调查的消费者数(人) | 200 | 500 | 200 | 70 | 30 |
注:每组包含最小值不包含最大值,且住房面积取整数.
请你根据以上信息,回答下列问题:
(1)根据表格可得,被调查的消费者平均年收入为2.39万元;被调查的消费者中年收入的中位数是1.8;在平均数与中位数这两个数中,中位数更能反映被调查的消费者年收入的一般水平.
(2)根据频数分布直方图可得,打算购买100-120m2房子的人数为240人;打算购买住房面积小于100m2的消费者占被调查消费者人数的百分数是52%.
(3)在图中补全这个频数分布直方图.
 如图,正方形ABCD,曲线DP1P2P3P4P5…叫做“正方形的渐开线”,其中弧DP1,弧P1P2,弧P2P3,弧P3P4,弧P4P5…的圆心依次按点A,B,C,D,A循环,它们的弧长分别记为l1,l2,l3,l4,l5….当AB=1时,l2011等于$\frac{2011π}{2}$.
如图,正方形ABCD,曲线DP1P2P3P4P5…叫做“正方形的渐开线”,其中弧DP1,弧P1P2,弧P2P3,弧P3P4,弧P4P5…的圆心依次按点A,B,C,D,A循环,它们的弧长分别记为l1,l2,l3,l4,l5….当AB=1时,l2011等于$\frac{2011π}{2}$.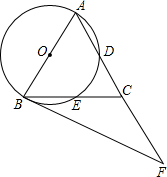 如图,在△ABC中,AB=AC,∠BAC=54°,以AB为直径的⊙O分别交AC,BC于点D、E,过点B作⊙O的切线,交AC的延长线于点F.
如图,在△ABC中,AB=AC,∠BAC=54°,以AB为直径的⊙O分别交AC,BC于点D、E,过点B作⊙O的切线,交AC的延长线于点F.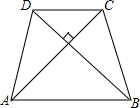 如图,等腰梯形ABCD的面积为100cm2,AC⊥BD.
如图,等腰梯形ABCD的面积为100cm2,AC⊥BD. 已知,等腰△ABC中,AB=AC,点D、E分别在边BC、AC上,且∠ADE=∠C,求证:△ABD∽△DCE.
已知,等腰△ABC中,AB=AC,点D、E分别在边BC、AC上,且∠ADE=∠C,求证:△ABD∽△DCE.