题目内容
19. 如图,在?ABCD中,E为CD中点,AE与BD相交于点O,S△DOE=3cm2,则S△ADB等于18cm2.
如图,在?ABCD中,E为CD中点,AE与BD相交于点O,S△DOE=3cm2,则S△ADB等于18cm2.
分析 利用平行四边形的性质得出AB=DC,AB∥CD,进而得出△DOE∽△BOA,再利用相似三角形的性质得出答案.
解答 解:∵四边形ABCD是平行四边形,
∴AB=DC,AB∥CD,
∴△DOE∽△BOA,
∴$\frac{OE}{OA}$=$\frac{DE}{AB}$,
∵E为CD中点,
∴$\frac{DE}{AB}$=$\frac{1}{2}$,
∴$\frac{OE}{OA}$=$\frac{1}{2}$,
∴$\frac{{S}_{△DOE}}{{S}_{△BOA}}$=$\frac{1}{4}$,$\frac{{S}_{△DOE}}{{S}_{△AOD}}$=$\frac{1}{2}$,
∵S△DOE=3cm2,∴S△AOB=12cm2,S△AOD=6cm2,
∴S△ADB=S△AOB+S△AOD=18cm2;
故答案为:18.
点评 此题主要考查了平行四边形的性质以及相似三角形的判定与性质,得出△DOE∽△BOA是解题关键.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
10.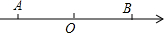 如图,数轴上两点A,B到原点O的距离相等,如果点A,B表示的数分别是x+3和x+7,那么线段OA的长度是( )
如图,数轴上两点A,B到原点O的距离相等,如果点A,B表示的数分别是x+3和x+7,那么线段OA的长度是( )
 如图,数轴上两点A,B到原点O的距离相等,如果点A,B表示的数分别是x+3和x+7,那么线段OA的长度是( )
如图,数轴上两点A,B到原点O的距离相等,如果点A,B表示的数分别是x+3和x+7,那么线段OA的长度是( )| A. | 2 | B. | x+5 | C. | -2 | D. | 4 |
4.经过点(-2,1)的反比例函数图象应在( )
| A. | 第一、三象限 | B. | 第二、四象限 | C. | 第二、三象限 | D. | 第一、二象限 |
8.七年级一班课外兴趣小组准备开会讨论问题,按如下方式摆放长书桌和椅子,发现一张长书桌边可以坐6个人,加一张长书桌时可以坐8个人,再加一张长书桌时可以坐10个人…

他们发现书桌和可坐人数数量变化有规律:(请把图表中的空格补充完整)

他们发现书桌和可坐人数数量变化有规律:(请把图表中的空格补充完整)
| 长桌张数 | 1 | 2 | 3 | 4 | … | n |
| 可坐人数 | 6 | 8 | 10 | 12 | … | 2n+4 |
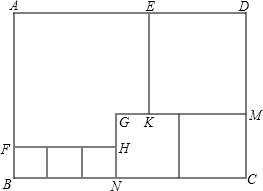 如图所示,用三种大小不等的正方形和一个缺角的正方形拼成一个长方形ABCD(不重叠且没有缝隙),若GH=GK=1,设BF=x.
如图所示,用三种大小不等的正方形和一个缺角的正方形拼成一个长方形ABCD(不重叠且没有缝隙),若GH=GK=1,设BF=x. 如图,正方形ABCD,曲线DP1P2P3P4P5…叫做“正方形的渐开线”,其中弧DP1,弧P1P2,弧P2P3,弧P3P4,弧P4P5…的圆心依次按点A,B,C,D,A循环,它们的弧长分别记为l1,l2,l3,l4,l5….当AB=1时,l2011等于$\frac{2011π}{2}$.
如图,正方形ABCD,曲线DP1P2P3P4P5…叫做“正方形的渐开线”,其中弧DP1,弧P1P2,弧P2P3,弧P3P4,弧P4P5…的圆心依次按点A,B,C,D,A循环,它们的弧长分别记为l1,l2,l3,l4,l5….当AB=1时,l2011等于$\frac{2011π}{2}$.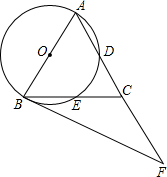 如图,在△ABC中,AB=AC,∠BAC=54°,以AB为直径的⊙O分别交AC,BC于点D、E,过点B作⊙O的切线,交AC的延长线于点F.
如图,在△ABC中,AB=AC,∠BAC=54°,以AB为直径的⊙O分别交AC,BC于点D、E,过点B作⊙O的切线,交AC的延长线于点F.