题目内容
4.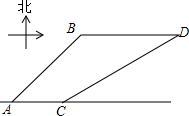 如图,港口B在港口A的东北方向,相距40$\sqrt{2}$海里,上午9时,一艘轮船从港口A出发,以15海里/时的速度向正东方向航行,同时一艘快艇从港口B出发也向正东方向航行,上午11时轮船到达C处,同时快艇到达D处,测试测得D在C的北偏东60°方向上,求快艇每小时航行多少海里?
如图,港口B在港口A的东北方向,相距40$\sqrt{2}$海里,上午9时,一艘轮船从港口A出发,以15海里/时的速度向正东方向航行,同时一艘快艇从港口B出发也向正东方向航行,上午11时轮船到达C处,同时快艇到达D处,测试测得D在C的北偏东60°方向上,求快艇每小时航行多少海里?
分析 分别过点B、D作AC的垂线,交AC于E、F,根据等腰直角三角形的性质求出AB,根据平行四边形的判定和性质求出DF,根据直角三角形的性质求出CF的长,求出BD,得到答案.
解答 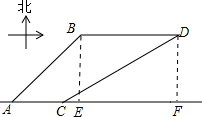 解:分别过点B、D作AC的垂线,交AC于E、F,
解:分别过点B、D作AC的垂线,交AC于E、F,
∵∠BEA=90°,∠BAE=45°,AB=40$\sqrt{2}$,
由勾股定理得,AE=BE=40,
∵BD∥EF,BE∥DF,
∴四边形BEFD是平行四边形,
∴DF=BE=40,
∵∠DFC=90°,∠DCF=30°,DF=40,
∴CF=40$\sqrt{3}$,
∴EF=AF-AE=40$\sqrt{3}$-10,
∴BD=EF=40$\sqrt{3}$-10,
快艇的速度为(40$\sqrt{3}$-10)÷2=20$\sqrt{3}$-5.
答:快艇的速度为20$\sqrt{3}$-5海里/时.
点评 本题考查的是解直角三角形的知识,掌握方向角问题,结合航海中的实际问题,将解直角三角形的相关知识有机结合是解题的关键.

练习册系列答案
相关题目
15.下列语句中正确的是( )
| A. | 边数越多的多边形,它的内角和也越大 | |
| B. | 多边形随着边数的增加,它的外角和和随着增加 | |
| C. | 当多边形的边数扩大两倍时,多边形的内角和也扩大两倍 | |
| D. | 当边数超过4时,多边形的内角一定大于相邻的外角 |
12.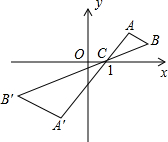 如图,△ABC中,A、B两个顶点在x轴的上方,点C的坐标是(1,0),以点C位似中心,在x轴的下方作△ABC的位似图形△A′B′C,并把△ABC的边长放大到原来的2倍,设点B的横坐标是a,则点B的对应点B′的横坐标是( )
如图,△ABC中,A、B两个顶点在x轴的上方,点C的坐标是(1,0),以点C位似中心,在x轴的下方作△ABC的位似图形△A′B′C,并把△ABC的边长放大到原来的2倍,设点B的横坐标是a,则点B的对应点B′的横坐标是( )
 如图,△ABC中,A、B两个顶点在x轴的上方,点C的坐标是(1,0),以点C位似中心,在x轴的下方作△ABC的位似图形△A′B′C,并把△ABC的边长放大到原来的2倍,设点B的横坐标是a,则点B的对应点B′的横坐标是( )
如图,△ABC中,A、B两个顶点在x轴的上方,点C的坐标是(1,0),以点C位似中心,在x轴的下方作△ABC的位似图形△A′B′C,并把△ABC的边长放大到原来的2倍,设点B的横坐标是a,则点B的对应点B′的横坐标是( )| A. | -2a | B. | 2a-2 | C. | 3-2a | D. | 2a-3 |
19.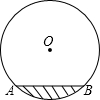 在圆柱形油槽内装有一些油,截面如图,油面宽AB为6cm,如果再注入一些油后,油面上升1m,油面宽度为8m,圆柱形油槽的直径为( )
在圆柱形油槽内装有一些油,截面如图,油面宽AB为6cm,如果再注入一些油后,油面上升1m,油面宽度为8m,圆柱形油槽的直径为( )
 在圆柱形油槽内装有一些油,截面如图,油面宽AB为6cm,如果再注入一些油后,油面上升1m,油面宽度为8m,圆柱形油槽的直径为( )
在圆柱形油槽内装有一些油,截面如图,油面宽AB为6cm,如果再注入一些油后,油面上升1m,油面宽度为8m,圆柱形油槽的直径为( )| A. | 6m | B. | 8m | C. | 10m | D. | 12m |
13. 如图,已知:∠1=∠2,∠D=50°,则∠B的度数是( )
如图,已知:∠1=∠2,∠D=50°,则∠B的度数是( )
 如图,已知:∠1=∠2,∠D=50°,则∠B的度数是( )
如图,已知:∠1=∠2,∠D=50°,则∠B的度数是( )| A. | 50° | B. | 130° | ||
| C. | 150° | D. | 以上结果均不正确 |
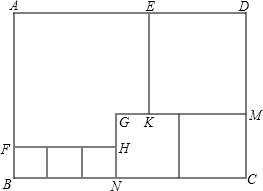 如图所示,用三种大小不等的正方形和一个缺角的正方形拼成一个长方形ABCD(不重叠且没有缝隙),若GH=GK=1,设BF=x.
如图所示,用三种大小不等的正方形和一个缺角的正方形拼成一个长方形ABCD(不重叠且没有缝隙),若GH=GK=1,设BF=x.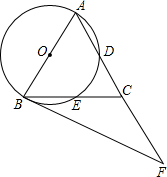 如图,在△ABC中,AB=AC,∠BAC=54°,以AB为直径的⊙O分别交AC,BC于点D、E,过点B作⊙O的切线,交AC的延长线于点F.
如图,在△ABC中,AB=AC,∠BAC=54°,以AB为直径的⊙O分别交AC,BC于点D、E,过点B作⊙O的切线,交AC的延长线于点F.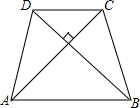 如图,等腰梯形ABCD的面积为100cm2,AC⊥BD.
如图,等腰梯形ABCD的面积为100cm2,AC⊥BD.