题目内容
20.小励同学有面额10元.20元.50元和100元的纸币各一张,分别装入大小外观完全样的四个红包中,每个红包里只装入一张纸币,若小励从中随机抽取两个红包.(1)请用树状图或者列表的方法,求小励取出纸币的总额为70元的概率;
(2)求小励取出纸币的总额能购买一件价格为120元文具的概率.
分析 (1)先利用树状图展示所有12种等可能的结果数,再找出取出纸币的总额为70元的结果数,然后根据概率公式计算;
(2)根据(1)中树状图找到取出纸币的总额大于或等于120元的结果数,根据概率公式计算可得.
解答 解:(1)画树状图为:
共有12种等可能的结果数,其中取出纸币的总额为70元的结果数为2,
所以取出纸币的总额为70元的概率=$\frac{2}{12}$=$\frac{1}{6}$;
(2)小励取出纸币的总额能购买一件价格为120元文具的概率为$\frac{4}{12}$=$\frac{1}{3}$.
点评 本题考查了列表法与树状图法:利用列表法和树状图法展示所有可能的结果求出n,再从中选出符合事件A或B的结果数目m,求出概率.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.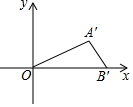 如图,平面直角坐标系中,以原点O为位似中心,按相似比为1:2将△OAB放大后得到△OA′B′,若点A的对应点A′的坐标为(4,2),则点A的坐标为( )
如图,平面直角坐标系中,以原点O为位似中心,按相似比为1:2将△OAB放大后得到△OA′B′,若点A的对应点A′的坐标为(4,2),则点A的坐标为( )
 如图,平面直角坐标系中,以原点O为位似中心,按相似比为1:2将△OAB放大后得到△OA′B′,若点A的对应点A′的坐标为(4,2),则点A的坐标为( )
如图,平面直角坐标系中,以原点O为位似中心,按相似比为1:2将△OAB放大后得到△OA′B′,若点A的对应点A′的坐标为(4,2),则点A的坐标为( )| A. | (2,1) | B. | (8,4) | C. | (2,1)或(-2,-1) | D. | (8,4)或(-8,-4) |
8. 如图,已知直线AB、CD相交于点O,OE平分∠COB,若∠EOB=55°,则∠AOC=( )
如图,已知直线AB、CD相交于点O,OE平分∠COB,若∠EOB=55°,则∠AOC=( )
 如图,已知直线AB、CD相交于点O,OE平分∠COB,若∠EOB=55°,则∠AOC=( )
如图,已知直线AB、CD相交于点O,OE平分∠COB,若∠EOB=55°,则∠AOC=( )| A. | 35° | B. | 55° | C. | 70° | D. | 110° |
15.下列命题中:①有公共顶点和一条公共边的两个角一定是邻补角;②垂线段最短;③经过直线外一点,有且只有一条直线与这条直线平行;④相等的角是对顶角;⑤等角的余角相等,其中假命题的个数是( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
10.下列计算正确的是( )
| A. | $\sqrt{27}$$÷\sqrt{3}$=3 | B. | 3+$\sqrt{3}$=3$\sqrt{3}$ | C. | $\sqrt{2}+\sqrt{3}$=$\sqrt{5}$ | D. | $\sqrt{(-2)^{2}}$=-2 |
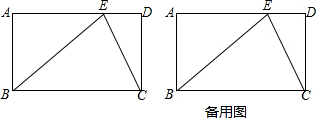
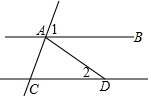 如图,已知直线AB∥CD,且线段AD=CD,若∠1=75°,则∠2的度数是30°.
如图,已知直线AB∥CD,且线段AD=CD,若∠1=75°,则∠2的度数是30°. 如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为10cm,则图中标记为正方形A,B,C,D的面积之和为100cm2.
如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为10cm,则图中标记为正方形A,B,C,D的面积之和为100cm2.