题目内容
11.如图,已知在矩形ABCD中,点E在AD边上,AE>DE,BE=BC.(1)试说明CE平分∠BED.
(2)若AB=3,BC=5,求CE的长.
(3)在直线AD上是否存在点F,使得以B,C,F,E为顶点的四边形是菱形?如果存在,试画出点F的位置,并作适当说明;如果不存在,请说明理由.
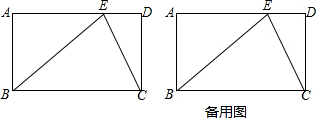
分析 (1)由矩形的性质得出∠A=∠D=90°,AD∥BC,AD=BC,CD=AB,由平行线的性质得出∠DEC=∠BCE,由等腰三角形的性质得出∠BCE=∠BEC,证出∠DEC=∠BEC,即可得出结论.
(2)由勾股定理求出AE=$\sqrt{B{E}^{2}-A{B}^{2}}$=4,得出DE=AD-AE=1,再由勾股定理求出CE即可;
(3)作BF⊥CE,交直线AD于F,由等腰三角形的性质得出BF平分CE,BF平分∠CBE,由垂直平分线的性质得出EF=CF,证出∠EFB=∠EBF,得出BE=EF,因此BE=BC=EF=CF,即可得出四边形BCFE是菱形.
解答 (1)证明:∵四边形ABCD是矩形,
∴∠A=∠D=90°,AD∥BC,AD=BC,CD=AB,
∴∠DEC=∠BCE,
∵BE=BC,
∴∠BCE=∠BEC,
∴∠DEC=∠BEC,
∴CE平分∠BED.
(2)解:∵∠A=90°,AB=3,BE=BC=5,
∴AE=$\sqrt{B{E}^{2}-A{B}^{2}}$=4,
∵AD=BC=5,
∴DE=AD-AE=1,
∵CD=AB=3,∠D=90°,
∴CE=$\sqrt{C{D}^{2}+D{E}^{2}}$=$\sqrt{{3}^{2}+{1}^{2}}$=$\sqrt{10}$;
(3)解:在直线AD上存在点F,使得以B,C,F,E为顶点的四边形是菱形;
作BF⊥CE,交直线AD于F,如图所示:
理由如下:
∵BE=BC,BF⊥CE,
∴BF平分CE,BF平分∠CBE,
∴EF=CF,
∵AF∥BC,
∴∠EFB=∠CBF,
∴∠EFB=∠EBF,
∴BE=EF,
∴BE=BC=EF=CF,
∴四边形BCFE是菱形.
点评 本题考查了矩形的性质、勾股定理、等腰三角形的判定、菱形的判定等知识;熟练掌握矩形的性质和等腰三角形的判定是解决问题的关键.

 名校课堂系列答案
名校课堂系列答案 如图,在△ABC中,∠C=90°,点D在BC上,AD=BD=5,cos∠ADC=$\frac{3}{4}$.
如图,在△ABC中,∠C=90°,点D在BC上,AD=BD=5,cos∠ADC=$\frac{3}{4}$. 如图,若△AOB≌△COD,∠B=30°,∠AOC=52°,则∠CEO的度数为82°.
如图,若△AOB≌△COD,∠B=30°,∠AOC=52°,则∠CEO的度数为82°.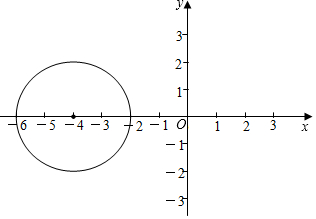 如图,在平面直角坐标系中,点P的坐标为(-4,0),⊙P的半径为2,将⊙P沿x轴向右平移4个单位长度得
如图,在平面直角坐标系中,点P的坐标为(-4,0),⊙P的半径为2,将⊙P沿x轴向右平移4个单位长度得