题目内容
7．关于四边形ABCD：①两组对边分别相等；②一组对边平行且相等；③一组对边平行且另一组对边相等；④两条对角线相等．以上四种条件中，可以判定四边形ABCD是平行四边形的有（ ）| A． | ①②③④ | B． | ①③④ | C． | ①② | D． | ③④ |
分析 由平行四边形的判定定理得出①和②能判定四边形ABCD是平行四边形；③和④不一定能判定四边形ABCD是平行四边形；即可得出结论．
解答 解：∵两组对边分别相等的四边形是平行四边形，
∴①能判定；
∵一组对边平行且相等的四边形是平行四边形，
∴②能判定；
∵一组对边平行且另一组对边相等的四边形是梯形，不一定是平行四边形，
∴③不一定能；
∵两条对角线相等的四边形不一定是平行四边形，
∴④不一定能；
以上四种条件中，可以判定四边形ABCD是平行四边形的有①②；
故选：C．
点评 本题考查了平行四边形的判定方法；熟练掌握平行四边形的判定方法，不能进行推理论证是解决问题的关键．
练习册系列答案
名校课堂系列答案
相关题目
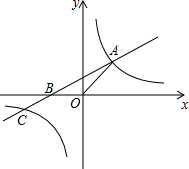如图，直线y=kx+2k（k≠0）与x轴交于点B，与双曲线y=$\frac{4}{x}$交于点A、C，其中点A在第一象限，点C在第三象限．
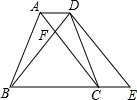如图所示，梯形ABCD中，已知：AD∥BC，∠ABC=∠DCB，对角线AC、BD相交于点F，点E是边BC延长线上一点，且∠CDE=∠ABD．
2．化简（$\sqrt{3}$-2）2015•（$\sqrt{3}$+2）2016的结果为（ ）
| A． | -1 | B． | $\sqrt{3}$-2 | C． | $\sqrt{3}$+2 | D． | -$\sqrt{3}$-2 |
16．
如图，AB是半圆O的直径，弦AD、BC相交于点P，若∠DPB=60°，则CD：AB等于（ ）
如图，AB是半圆O的直径，弦AD、BC相交于点P，若∠DPB=60°，则CD：AB等于（ ）| A． | $\frac{1}{2}$ | B． | $\frac{\sqrt{3}}{2}$ | C． | $\frac{\sqrt{3}}{3}$ | D． | $\sqrt{3}$ |
