题目内容
2．化简（$\sqrt{3}$-2）2015•（$\sqrt{3}$+2）2016的结果为（ ）| A． | -1 | B． | $\sqrt{3}$-2 | C． | $\sqrt{3}$+2 | D． | -$\sqrt{3}$-2 |
分析 先利用积的乘方得到原式=[（$\sqrt{3}$-2）•（$\sqrt{3}$+2）]2015•（$\sqrt{3}$+2），然后根据平方差公式计算．
解答 解：原式=[（$\sqrt{3}$-2）•（$\sqrt{3}$+2）]2015•（$\sqrt{3}$+2）
=（3-4）2015•（$\sqrt{3}$+2）
=-$\sqrt{3}$-2．
故选D．
点评 本题考查了二次根式的计算：先把各二次根式化为最简二次根式，再进行二次根式的乘除运算，然后合并同类二次根式．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
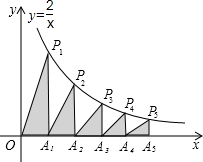如图，在x轴的正半轴上依次截取OA1=A1A2=A3A4=A4A5，过点A1、A2、A3、A4、A5分别作x轴的垂线与反比例函数的y=$\frac{2}{x}$（x≠0）的图象相交于点P1、P2、P3、P4、P5，得直角三角形OP1A1、A1P2A2、A2P3A3、A3P4A4、A4P5A5并设其面积分别为S1、S2、S3、S4、S5，则S5的值为$\frac{1}{5}$，以此类推Sn=$\frac{1}{n}$（n≥1的整数）
13．要使分式$\frac{x}{x+1}$有意义，则x应满足的条件是（ ）
| A． | x≠1 | B． | x≠-1 | C． | x≠0 | D． | x＞1 |
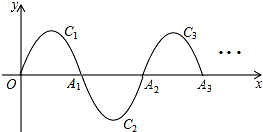如图，一段抛物线y=-x（x-3）（0≤x≤3），记为C1，它与x轴交于点O，A1；将C1绕点A1旋转180°得C2，交x 轴于点A2；将C2绕点A2旋转180°得C3，交x 轴于点A3；…如此进行下去，得到一条“波浪线”．若点P（37，m）在此“波浪线”上，则m的值为2．
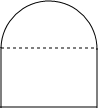刘师傅是货车司机，他的车高是2.9m、宽2.5m，这次他的运输任务要经过一个如图所示的涵洞．已知半圆拱的圆心距地面2m，半径1.5m，你认为刘师傅能通过这个涵洞吗？
7．关于四边形ABCD：①两组对边分别相等；②一组对边平行且相等；③一组对边平行且另一组对边相等；④两条对角线相等．以上四种条件中，可以判定四边形ABCD是平行四边形的有（ ）
| A． | ①②③④ | B． | ①③④ | C． | ①② | D． | ③④ |
14．某校初三（1）班进行立定跳远训练，以下是李超和陈辉同学六次的训练成绩（单位：m）
（1）李超和陈辉的平均成绩分别是多少？
（2）分别计算两人的六次成绩的方差，哪个人的成绩更稳定？为什么？
（3）若预知参加级的比赛能跳过2.55米就可能得冠军，应选哪个同学参加？为什么？
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 李超 | 2.50 | 2.42 | 2.52 | 2.56 | 2.48 | 2.58 |
| 陈辉 | 2.54 | 2.48 | 2.50 | 2.48 | 2.54 | 2.52 |
（2）分别计算两人的六次成绩的方差，哪个人的成绩更稳定？为什么？
（3）若预知参加级的比赛能跳过2.55米就可能得冠军，应选哪个同学参加？为什么？
画图并回答．