题目内容
18.计算(1)(-$\frac{3x}{2y}$)•$\frac{2y}{{x}^{3}}$;
(2)(a-$\frac{2a-1}{a}$)÷$\frac{1-{a}^{2}}{{a}^{2}+a}$.
分析 (1)原式约分即可得到结果;
(2)原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分即可得到结果.
解答 解:(1)原式=-$\frac{3}{{x}^{2}}$;
(2)原式=$\frac{{a}^{2}-2a+1}{a}$•$\frac{a(a+1)}{-(a+1)(a-1)}$
=-$\frac{(a-1)^{2}}{a}$•$\frac{a(a+1)}{(a+1)(a-1)}$
=-a+1.
点评 此题考查了分式的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 学习实践园地系列答案
学习实践园地系列答案
相关题目
13.要使分式$\frac{x}{x+1}$有意义,则x应满足的条件是( )
| A. | x≠1 | B. | x≠-1 | C. | x≠0 | D. | x>1 |
7.关于四边形ABCD:①两组对边分别相等;②一组对边平行且相等;③一组对边平行且另一组对边相等;④两条对角线相等.以上四种条件中,可以判定四边形ABCD是平行四边形的有( )
| A. | ①②③④ | B. | ①③④ | C. | ①② | D. | ③④ |
8.下列命题中正确的是( )
| A. | 对角线相等的四边形是矩形 | |
| B. | 对角线互相平分且相等的四边形是正方形 | |
| C. | 对角线互相垂直的四边形是菱形 | |
| D. | 对角线互相垂直平分的四边形是菱形 |
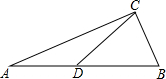 如图,在△ABC中,∠ACB=90°,∠A=15°,AB=8cm,CD为AB的中线,求△ABC的面积.
如图,在△ABC中,∠ACB=90°,∠A=15°,AB=8cm,CD为AB的中线,求△ABC的面积.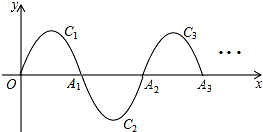 如图,一段抛物线y=-x(x-3)(0≤x≤3),记为C1,它与x轴交于点O,A1;将C1绕点A1旋转180°得C2,交x 轴于点A2;将C2绕点A2旋转180°得C3,交x 轴于点A3;…如此进行下去,得到一条“波浪线”.若点P(37,m)在此“波浪线”上,则m的值为2.
如图,一段抛物线y=-x(x-3)(0≤x≤3),记为C1,它与x轴交于点O,A1;将C1绕点A1旋转180°得C2,交x 轴于点A2;将C2绕点A2旋转180°得C3,交x 轴于点A3;…如此进行下去,得到一条“波浪线”.若点P(37,m)在此“波浪线”上,则m的值为2.