题目内容
19.解不等式组$\left\{\begin{array}{l}{2x+5≤3(x+2)}\\{\frac{x-1}{2}<\frac{x}{3}}\end{array}\right.$并写出它的所有的整数解.分析 首先解每个不等式,两个不等式的解集的公共部分就是不等式组的解集,然后确定整数解即可.
解答 解:$\left\{\begin{array}{l}{2x+5≤3(x+2)…①}\\{\frac{x-1}{2}<\frac{x}{3}…②}\end{array}\right.$,
解①得:x≥-1,
解②得:x<3.
则不等式组的解集是:-1≤x<3.
则整数解是:-1,0,1,2.
点评 本题考查的是一元一次不等式组的解,解此类题目常常要结合数轴来判断.还可以观察不等式的解,若x>较小的数、<较大的数,那么解集为x介于两数之间.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
7.关于四边形ABCD:①两组对边分别相等;②一组对边平行且相等;③一组对边平行且另一组对边相等;④两条对角线相等.以上四种条件中,可以判定四边形ABCD是平行四边形的有( )
| A. | ①②③④ | B. | ①③④ | C. | ①② | D. | ③④ |
14.某校初三(1)班进行立定跳远训练,以下是李超和陈辉同学六次的训练成绩(单位:m)
(1)李超和陈辉的平均成绩分别是多少?
(2)分别计算两人的六次成绩的方差,哪个人的成绩更稳定?为什么?
(3)若预知参加级的比赛能跳过2.55米就可能得冠军,应选哪个同学参加?为什么?
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 李超 | 2.50 | 2.42 | 2.52 | 2.56 | 2.48 | 2.58 |
| 陈辉 | 2.54 | 2.48 | 2.50 | 2.48 | 2.54 | 2.52 |
(2)分别计算两人的六次成绩的方差,哪个人的成绩更稳定?为什么?
(3)若预知参加级的比赛能跳过2.55米就可能得冠军,应选哪个同学参加?为什么?
4.把$\frac{\sqrt{3a}}{\sqrt{12ab}}$化简后得( )
| A. | 4b | B. | $2\sqrt{b}$ | C. | $\frac{1}{2}\sqrt{b}$ | D. | $\frac{{\sqrt{b}}}{2b}$ |
8.下列命题中正确的是( )
| A. | 对角线相等的四边形是矩形 | |
| B. | 对角线互相平分且相等的四边形是正方形 | |
| C. | 对角线互相垂直的四边形是菱形 | |
| D. | 对角线互相垂直平分的四边形是菱形 |
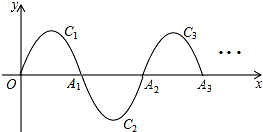 如图,一段抛物线y=-x(x-3)(0≤x≤3),记为C1,它与x轴交于点O,A1;将C1绕点A1旋转180°得C2,交x 轴于点A2;将C2绕点A2旋转180°得C3,交x 轴于点A3;…如此进行下去,得到一条“波浪线”.若点P(37,m)在此“波浪线”上,则m的值为2.
如图,一段抛物线y=-x(x-3)(0≤x≤3),记为C1,它与x轴交于点O,A1;将C1绕点A1旋转180°得C2,交x 轴于点A2;将C2绕点A2旋转180°得C3,交x 轴于点A3;…如此进行下去,得到一条“波浪线”.若点P(37,m)在此“波浪线”上,则m的值为2. 如图,点D、E是腰长为5的等腰三角形ABC两腰的中点,P为底边BC上一点,则PD+PE的最小值为5.
如图,点D、E是腰长为5的等腰三角形ABC两腰的中点,P为底边BC上一点,则PD+PE的最小值为5.