题目内容
15.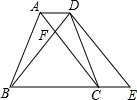 如图所示,梯形ABCD中,已知:AD∥BC,∠ABC=∠DCB,对角线AC、BD相交于点F,点E是边BC延长线上一点,且∠CDE=∠ABD.
如图所示,梯形ABCD中,已知:AD∥BC,∠ABC=∠DCB,对角线AC、BD相交于点F,点E是边BC延长线上一点,且∠CDE=∠ABD.(1)求证:四边形ACED是平行四边形;
(2)若△ADF的面积是2cm2,且BC=3AD,求梯形ABCD的面积.
分析 (1)根据梯形的性质和已知证明四边形ABCD为等腰梯形,根据等腰梯形的性质证明△ABD≌△DCA,得到∠ABD=∠DCA,根据平行线的判定定理证明结论;
(2)根据相似三角形的性质求出$\frac{DF}{BF}$、$\frac{AF}{CF}$的值,根据三角形的面积公式和相似三角形的性质求出梯形ABCD的面积.
解答 解:∵AD∥BC,∠ABC=∠DCB,
∴四边形ABCD为等腰梯形,
∴AB=CD,AC=BD,
在△ABD和△DCA中,
$\left\{\begin{array}{l}{AB=DC}\\{AC=DB}\\{AD=AD}\end{array}\right.$,
∴△ABD≌△DCA,
∴∠ABD=∠DCA,又∠CDE=∠ABD,
∴∠DCA=∠CDE,
∴AC∥DE,
又∵AD∥BC,
∴四边形ACED是平行四边形;
(2)∵AD∥BC,
∴△ADF∽△CBF,
∴$\frac{DF}{BF}$=$\frac{AF}{CF}$=$\frac{AD}{BC}$=$\frac{1}{3}$,
∵△ADF的面积是2cm2,
∴△ABF的面积是6cm2,△DCF的面积是6cm2,△BCF的面积是18cm2,
∴梯形ABCD的面积为2+6+6+18=32cm2.
点评 本题考查的是梯形的性质、等腰梯形的判定和性质、平行四边形的判定和相似三角形的性质,掌握相关的判定定理和性质定理是解题的关键.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案
相关题目
5.已知点A(x1,y1)、B(x2,y2)、C(x3,y3)是函数y=-$\frac{2}{x}$图象上的点,且x1<0<x2<x3,则y1,y2,y3的大小关系是( )
| A. | y1>y2>y3 | B. | y1<y2<y3 | C. | y1>y3>y2 | D. | 无法确定 |
20.计算:210+(-2)10,下面结果正确的是( )
| A. | 0 | B. | 20 | C. | 410 | D. | 211 |
7.关于四边形ABCD:①两组对边分别相等;②一组对边平行且相等;③一组对边平行且另一组对边相等;④两条对角线相等.以上四种条件中,可以判定四边形ABCD是平行四边形的有( )
| A. | ①②③④ | B. | ①③④ | C. | ①② | D. | ③④ |
4.把$\frac{\sqrt{3a}}{\sqrt{12ab}}$化简后得( )
| A. | 4b | B. | $2\sqrt{b}$ | C. | $\frac{1}{2}\sqrt{b}$ | D. | $\frac{{\sqrt{b}}}{2b}$ |
5.某铁皮加工厂准备用380张铁皮制作一批盒子,已知每张铁皮可做8个盒身或做22个盒底,而一个盒身与两个盒底配成一个盒子.设用x张铁皮做盒身,y张铁皮做盒底,可以正好制成一批完整的盒子,则( )
| A. | $\left\{\begin{array}{l}{x+y=380}\\{8x=22y}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+y=380}\\{2×8x=22y}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{x+y=380}\\{8x=2×22y}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x+y=380}\\{22x=8y}\end{array}\right.$ |
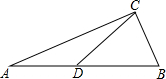 如图,在△ABC中,∠ACB=90°,∠A=15°,AB=8cm,CD为AB的中线,求△ABC的面积.
如图,在△ABC中,∠ACB=90°,∠A=15°,AB=8cm,CD为AB的中线,求△ABC的面积.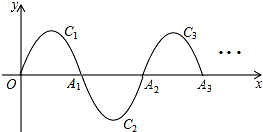 如图,一段抛物线y=-x(x-3)(0≤x≤3),记为C1,它与x轴交于点O,A1;将C1绕点A1旋转180°得C2,交x 轴于点A2;将C2绕点A2旋转180°得C3,交x 轴于点A3;…如此进行下去,得到一条“波浪线”.若点P(37,m)在此“波浪线”上,则m的值为2.
如图,一段抛物线y=-x(x-3)(0≤x≤3),记为C1,它与x轴交于点O,A1;将C1绕点A1旋转180°得C2,交x 轴于点A2;将C2绕点A2旋转180°得C3,交x 轴于点A3;…如此进行下去,得到一条“波浪线”.若点P(37,m)在此“波浪线”上,则m的值为2.