题目内容
20. 如图,在△ABC中,∠B=30°,BC的垂直平分线交AB于点E,垂足为D,CE平分∠ACB,若BE=4,则AE的长为( )
如图,在△ABC中,∠B=30°,BC的垂直平分线交AB于点E,垂足为D,CE平分∠ACB,若BE=4,则AE的长为( )| A. | 1 | B. | 1.5 | C. | 2 | D. | 2.5 |
分析 根据线段的垂直平分线的性质得到EC=EB=4,根据直角三角形的性质计算即可.
解答 解:∵DE是BC的垂直平分线,
∴EC=EB=4,
∴∠ECB=∠B=30°,
∵CE平分∠ACB,
∴∠ECB=∠ACE=30°,
∴∠A=90°,又∠ACE=30°,
∴AE=$\frac{1}{2}$EC=2,
故选C.
点评 本题考查的是线段的垂直平分线的性质,掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
5.如图,AB是⊙O的直径,点C在AB的延长线上,CD与⊙O相切,切点为D,如果∠A=35°,那么∠C=( )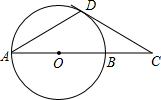

| A. | 55° | B. | 35° | C. | 30° | D. | 20° |

 用边长为a的正方形纸板,制成如图①的一幅七巧板,将它拼成如图②的“小天鹅”图案,其中阴影部分的面积为6cm2,那么a=4cm.
用边长为a的正方形纸板,制成如图①的一幅七巧板,将它拼成如图②的“小天鹅”图案,其中阴影部分的面积为6cm2,那么a=4cm.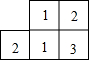 如图是由几个小立方块所搭几何体的从上面看到的形状图,小正方形中的数字表示在该位置小立方块的个数,请画出从正面,左面看到的这个几何体的形状图.
如图是由几个小立方块所搭几何体的从上面看到的形状图,小正方形中的数字表示在该位置小立方块的个数,请画出从正面,左面看到的这个几何体的形状图. 如图所示,以Rt△ABC的直角边BC为直径向外作半圆,则该半圆的面积为18π.
如图所示,以Rt△ABC的直角边BC为直径向外作半圆,则该半圆的面积为18π.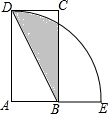 如图,四边形ABCD为矩形,以A为圆心,AD为半径的弧交AB的延长线于点E,连接BD,若AD=2AB=4,则图中阴影部分的面积为$\frac{4}{3}$π+2$\sqrt{3}$-4.
如图,四边形ABCD为矩形,以A为圆心,AD为半径的弧交AB的延长线于点E,连接BD,若AD=2AB=4,则图中阴影部分的面积为$\frac{4}{3}$π+2$\sqrt{3}$-4.