题目内容
15.要用反证法证明命题“在直角三角形中,至少有一个锐角不大于45°”,首先应假设两个锐角都大于45°.分析 反证法的步骤中,第一步是假设结论不成立,反面成立,可据此进行解答.
解答 解:“在直角三角形中,至少有一个锐角不大于45°”时应第一步先假设所求证的结论不成立,即为:两个锐角都大于45°.
故答案是:两个锐角都大于45°.
点评 本题结合角的比较考查反证法,解此题关键要懂得反证法的意义及步骤.在假设结论不成立时要注意考虑结论的反面所有可能的情况,如果只有一种,那么否定一种就可以了,如果有多种情况,则必须一一否定.

练习册系列答案
相关题目
3.用平面去截一个立方体,截面不可能是( )
| A. | 正方形 | B. | 五边形 | C. | 六边形 | D. | 七边形 |
10.已知某水库的警戒水位为18.8m,值班人员记录了某一周内的水位变化情况,如下表:(单位:m,上周末刚好到达警戒水位,取警戒水位为0,“+”表示水位比前一天升高,“-”表示水位比前一天降低)
(1)本周内哪一天水位最高?哪一天水位最低?它们与警戒水位相差多少?
(2)若超过警戒水位1.5m时就应该开闸放水,以确保大坝安全,本周水库需开闸放水吗?
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 变化情况(m) | +0.3 | +0.4 | -0.2 | +0.3 | +0.4 | -0.1 | -0.5 |
(2)若超过警戒水位1.5m时就应该开闸放水,以确保大坝安全,本周水库需开闸放水吗?
20. 如图,在△ABC中,∠B=30°,BC的垂直平分线交AB于点E,垂足为D,CE平分∠ACB,若BE=4,则AE的长为( )
如图,在△ABC中,∠B=30°,BC的垂直平分线交AB于点E,垂足为D,CE平分∠ACB,若BE=4,则AE的长为( )
 如图,在△ABC中,∠B=30°,BC的垂直平分线交AB于点E,垂足为D,CE平分∠ACB,若BE=4,则AE的长为( )
如图,在△ABC中,∠B=30°,BC的垂直平分线交AB于点E,垂足为D,CE平分∠ACB,若BE=4,则AE的长为( )| A. | 1 | B. | 1.5 | C. | 2 | D. | 2.5 |
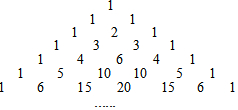 杨辉是我国南宋时期杰出的数学家和教育家,如图是杨辉在公元1261年著作《详解九章算法》里面的一张图,即“杨辉三角”,该图中有很多规律,请仔细观察,解答下列问题:
杨辉是我国南宋时期杰出的数学家和教育家,如图是杨辉在公元1261年著作《详解九章算法》里面的一张图,即“杨辉三角”,该图中有很多规律,请仔细观察,解答下列问题: 如图,点D、E、F分别是BC、AD、BC的中点,若△ABC的面积是20,则△BEF的面积为5.
如图,点D、E、F分别是BC、AD、BC的中点,若△ABC的面积是20,则△BEF的面积为5.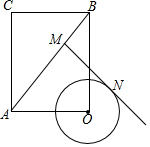 如图,在矩形AOBC中,AO=3,BO=4,⊙O的半径为1,点M是矩形对角线AB边上的动点,过点M做⊙O的一条切线MN,切点为N,则切线长MN的最小值是$\frac{\sqrt{119}}{5}$.
如图,在矩形AOBC中,AO=3,BO=4,⊙O的半径为1,点M是矩形对角线AB边上的动点,过点M做⊙O的一条切线MN,切点为N,则切线长MN的最小值是$\frac{\sqrt{119}}{5}$. 如图,AB∥CD,点E在线段BC上,若∠1=40°,∠2=30°,则∠3的度数是70°.
如图,AB∥CD,点E在线段BC上,若∠1=40°,∠2=30°,则∠3的度数是70°.