题目内容
9.实数范围内因式分解:2x2+4xy-3y2=(x+$\frac{-2y+\sqrt{10}y}{2}$)(x-$\frac{-2y-\sqrt{10}y}{2}$).分析 将原式在实数范围内分解即可.
解答 解:令2x2+4xy-3y2=0,
解得:x=$\frac{-4y±\sqrt{40{y}^{2}}}{4}$=$\frac{-2y±\sqrt{10}y}{2}$,
则原式=(x+$\frac{-2y+\sqrt{10}y}{2}$)(x-$\frac{-2y-\sqrt{10}y}{2}$),
故答案为:(x+$\frac{-2y+\sqrt{10}y}{2}$)(x-$\frac{-2y-\sqrt{10}y}{2}$)
点评 此题考查了实数范围内分解因式,熟练掌握因式分解的方法是解本题的关键.

练习册系列答案
相关题目
20. 如图,在△ABC中,∠B=30°,BC的垂直平分线交AB于点E,垂足为D,CE平分∠ACB,若BE=4,则AE的长为( )
如图,在△ABC中,∠B=30°,BC的垂直平分线交AB于点E,垂足为D,CE平分∠ACB,若BE=4,则AE的长为( )
 如图,在△ABC中,∠B=30°,BC的垂直平分线交AB于点E,垂足为D,CE平分∠ACB,若BE=4,则AE的长为( )
如图,在△ABC中,∠B=30°,BC的垂直平分线交AB于点E,垂足为D,CE平分∠ACB,若BE=4,则AE的长为( )| A. | 1 | B. | 1.5 | C. | 2 | D. | 2.5 |
 如图,AB∥CD,点E在线段BC上,若∠1=40°,∠2=30°,则∠3的度数是70°.
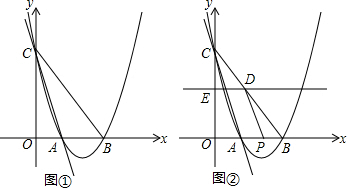
如图,AB∥CD,点E在线段BC上,若∠1=40°,∠2=30°,则∠3的度数是70°.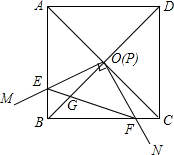 如图,边长为1的正方形ABCD的对角线AC,BD相交于点O,直角∠MPN的顶点P与点O重合,直角边PM,PN分别与OA,OB重合,然后逆时针旋转∠MPN,旋转角为θ(0°<θ<90°),PM、PN分别交AB、BC于E、F两点,连接EF交OB于点G,则下列结论中正确的是(1)(2)(4).
如图,边长为1的正方形ABCD的对角线AC,BD相交于点O,直角∠MPN的顶点P与点O重合,直角边PM,PN分别与OA,OB重合,然后逆时针旋转∠MPN,旋转角为θ(0°<θ<90°),PM、PN分别交AB、BC于E、F两点,连接EF交OB于点G,则下列结论中正确的是(1)(2)(4). 已知△ABC,如图所示.
已知△ABC,如图所示.