题目内容
12．
如图所示，以Rt△ABC的直角边BC为直径向外作半圆，则该半圆的面积为18π．
分析 根据勾股定理在Rt△ACB中可求BC，再根据圆的面积可求面积即可求解．
解答 解：在Rt△ACB中，BC=$\sqrt{A{B}^{2}-A{C}^{2}}$=12，
该半圆的面积为π×（12÷2）2÷2=18π．
故答案为：18π．
点评 考查了勾股定理，圆的面积，关键是勾股定理在Rt△ACB中求得BC．
练习册系列答案
相关题目
2．一辆小车由静止开始从光滑的斜面上向下滑动，通过观察记录小车滑动的距离s（m）与时间t（s）的数据如下表：
则写出用t表示s的关系式s=2t2．
| 时间t（s） | 1 | 2 | 3 | 4 | |
| 距离s（m） | 2 | 8 | 18 | 32 | … |
3．用平面去截一个立方体，截面不可能是（ ）
| A． | 正方形 | B． | 五边形 | C． | 六边形 | D． | 七边形 |
20．
如图，在△ABC中，∠B=30°，BC的垂直平分线交AB于点E，垂足为D，CE平分∠ACB，若BE=4，则AE的长为（ ）
如图，在△ABC中，∠B=30°，BC的垂直平分线交AB于点E，垂足为D，CE平分∠ACB，若BE=4，则AE的长为（ ）| A． | 1 | B． | 1.5 | C． | 2 | D． | 2.5 |
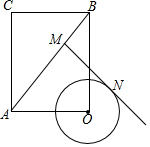如图，在矩形AOBC中，AO=3，BO=4，⊙O的半径为1，点M是矩形对角线AB边上的动点，过点M做⊙O的一条切线MN，切点为N，则切线长MN的最小值是$\frac{\sqrt{119}}{5}$．
如图，AB∥CD，点E在线段BC上，若∠1=40°，∠2=30°，则∠3的度数是70°．
如图，将长方形纸片ABCD沿BE翻折，使点C落在点F处，若∠DEF=40°，则∠FBE的度数为20°．