题目内容
6.若b=2a+3c,则抛物线y=ax2+bx+c与x轴的公共点的个数是2.分析 运用判别式进行分析即可.
解答 解:抛物线y=ax2+bx+c,b=2a+3c,
△=b2-4ac=4a2+12ac+9c2-4ac=(2a+2c)2+5c2,
当b≠0时,△>0,此时抛物线与x轴由两个交点,
当b=0时,2a+3c=0,由于a≠0,可得c≠0,此时:y=ax2+c,与x轴由2个交点,
综上所述,抛物线y=ax2+bx+c与x轴的公共点的个数是2,
故答案为:2.
点评 此题主要考查抛物线与x轴的交点问题,会灵活运用判别式是解题的关键.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
19. 由一些大小相同的小正方体组成的几何体主视图和俯视图如图所示,小正方体的块数可能有( )种.
由一些大小相同的小正方体组成的几何体主视图和俯视图如图所示,小正方体的块数可能有( )种.
 由一些大小相同的小正方体组成的几何体主视图和俯视图如图所示,小正方体的块数可能有( )种.
由一些大小相同的小正方体组成的几何体主视图和俯视图如图所示,小正方体的块数可能有( )种.| A. | 5种 | B. | 6种 | C. | 7种 | D. | 8种 |
15.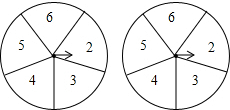 如图的两个圆盘中均有5个数字,同时旋转两个圆盘,指针落在某一个数上的机会均等,那么两个指针同时落在奇数上的概率是( )
如图的两个圆盘中均有5个数字,同时旋转两个圆盘,指针落在某一个数上的机会均等,那么两个指针同时落在奇数上的概率是( )
 如图的两个圆盘中均有5个数字,同时旋转两个圆盘,指针落在某一个数上的机会均等,那么两个指针同时落在奇数上的概率是( )
如图的两个圆盘中均有5个数字,同时旋转两个圆盘,指针落在某一个数上的机会均等,那么两个指针同时落在奇数上的概率是( )| A. | $\frac{4}{25}$ | B. | $\frac{6}{25}$ | C. | $\frac{10}{25}$ | D. | $\frac{19}{25}$ |
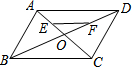 如图,在平行四边形ABCD中,AC与BD相交于点O,点E、F分别是OA、OD的中点,如果$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BO}$=$\overrightarrow{b}$,那么$\overrightarrow{EF}$=$\frac{1}{2}$$\overrightarrow{a}$+$\overrightarrow{b}$.
如图,在平行四边形ABCD中,AC与BD相交于点O,点E、F分别是OA、OD的中点,如果$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BO}$=$\overrightarrow{b}$,那么$\overrightarrow{EF}$=$\frac{1}{2}$$\overrightarrow{a}$+$\overrightarrow{b}$.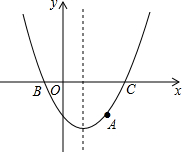 已知:二次函数的图象经过A(2,-3),对称轴x=1,抛物线与x轴两交点B、C的距离为4.
已知:二次函数的图象经过A(2,-3),对称轴x=1,抛物线与x轴两交点B、C的距离为4.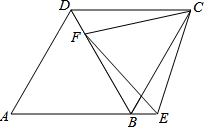 如图,在菱形ABCD中,F为对角线BD上一点,点E为AB延长线上一点,DF=BE,CE=CF.求证:
如图,在菱形ABCD中,F为对角线BD上一点,点E为AB延长线上一点,DF=BE,CE=CF.求证: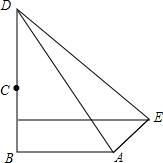 已知山顶上有一塔,山高BC为110米,小明在坡比为3:4的斜坡AE的底部A点测得塔顶D的仰角为45°,当他沿斜坡上行100米到达E时,测得塔顶D的仰角为19°,AB在同一水平线上,求塔高CD.(参考数据:tan19°≈0.35)
已知山顶上有一塔,山高BC为110米,小明在坡比为3:4的斜坡AE的底部A点测得塔顶D的仰角为45°,当他沿斜坡上行100米到达E时,测得塔顶D的仰角为19°,AB在同一水平线上,求塔高CD.(参考数据:tan19°≈0.35)