题目内容
14.(1)(-2xy3z2)2(2)a5•(-a)2÷a3
(3)(2x+3y)(3y-2x)+(x-3y)(x+3y)
(4)(-24x3y2+8x2y3-4x2y2)÷(-2xy)2
(5)(-2003)0×2$÷\frac{1}{2}$×$[(-\frac{1}{3})^{2}$÷23]
(6)(x-y+5)(x+y-5)
分析 (1)直接利用积的乘方运算法则求出答案;
(2)直接利用同底数幂的乘除法运算法则求出答案;
(3)直接利用平方差公式计算得出答案;
(4)直接利用多项式除以单项式进而求出答案;
(5)直接利用有理数混合运算法则化简求出答案;
(6)直接利用乘法公式将原式化简进而求出答案.
解答 解:(1)原式=4x2y6z4;
(2)原式=a5•a2÷a3=a4;
(3)原式=9y2-4x2+x2-9y2
=-3x2;
(4)原式=(-24x3y2+8x2y3-4x2y2)÷(4x2y2)
=-6x+2y-1;
(5)原式=1×2×2×($\frac{1}{9}$÷8)
=4×$\frac{1}{72}$
=$\frac{1}{18}$;
(6)原式=[x-(y-5)][x+(y-5)]
=x2-(y-5)2
=x2-y2+10y-25.
点评 此题主要考查了积的乘方运算以及整式的混合运算,正确掌握运算法则是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.某人向东行走5米,记作“+5米”,那么他向西行走3米,记作( )
| A. | “-3米” | B. | “+3米” | C. | “-8米” | D. | “+8米” |
3.在二次函数y=ax2+bx+c(a≠0)中,函数y与自变量x的部分对应值如下表:
当满足x<$\frac{1}{2}$时,y随x的增大而增大.
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
| y | 6 | 0 | -4 | -6 | -6 | -4 | 0 | 6 |
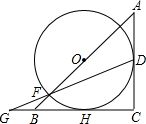 如图,在等腰直角三角形ABC中,以斜边AB的中点O为圆心的⊙O与AC相切于点D,与AB相交于点E,F,DF与CB的延长线交于点G.
如图,在等腰直角三角形ABC中,以斜边AB的中点O为圆心的⊙O与AC相切于点D,与AB相交于点E,F,DF与CB的延长线交于点G.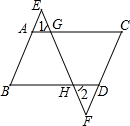 如图,已知点E,F分别在BA,CD的延长线上,连接EF,交AC,BD于G,H点,且∠1=∠2,∠B=∠C.
如图,已知点E,F分别在BA,CD的延长线上,连接EF,交AC,BD于G,H点,且∠1=∠2,∠B=∠C.