题目内容
18.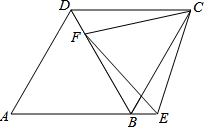 如图,在菱形ABCD中,F为对角线BD上一点,点E为AB延长线上一点,DF=BE,CE=CF.求证:
如图,在菱形ABCD中,F为对角线BD上一点,点E为AB延长线上一点,DF=BE,CE=CF.求证:(1)△CFD≌△CEB;
(2)∠CFE=60°.
分析 (1)根据菱形的性质得出CD=CB,又DF=BE,CF=CE,根据SSS即可证明△CFD≌△CEB;
(2)根据全等三角形、菱形的性质得出∠ABD=∠CBD=∠CDB=∠CBE,由平角的定义求出∠ABD=∠CBD=∠CBE=60°,再证明∠FCE=60°,那么由CF=CE,
得出△CFE是等边三角形,于是∠CFE=60°.
解答 (1)证明:∵四边形ABCD是菱形,
∴CD=CB.
在△CFD和△CEB中,
$\left\{\begin{array}{l}{CD=CB}\\{CF=CE}\\{DF=BE}\end{array}\right.$,
∴△CFD≌△CEB(SSS); (2)解:∵△CFD≌△CEB,
(2)解:∵△CFD≌△CEB,
∴∠CDB=∠CBE,∠DCF=∠BCE.
∵四边形ABCD是菱形,
∴∠CBD=∠ABD.
∵CD=CB,
∴∠CDB=∠CBD,
∴∠ABD=∠CBD=∠CBE=60°.
∴∠DCB=60°.
∵∠FCE=60°,
∵CF=CE,
∴∠CFE=∠CEF=60°.
点评 本题考查了菱形的性质:①菱形具有平行四边形的一切性质;②菱形的四条边都相等;③菱形的两条对角线互相垂直,并且每一条对角线平分一组对角;④菱形是轴对称图形,它有2条对称轴,分别是两条对角线所在直线.也考查了全等三角形、等边三角形的判定与性质.

练习册系列答案
相关题目
3.在二次函数y=ax2+bx+c(a≠0)中,函数y与自变量x的部分对应值如下表:
当满足x<$\frac{1}{2}$时,y随x的增大而增大.
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
| y | 6 | 0 | -4 | -6 | -6 | -4 | 0 | 6 |
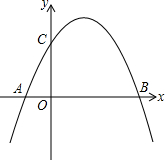 如图,抛物线y=-x2+bx+c与x轴交于AB两点(A在B的左侧),与y轴相交于点C(0,3),抛物线的顶点在第一象限,AB=4.
如图,抛物线y=-x2+bx+c与x轴交于AB两点(A在B的左侧),与y轴相交于点C(0,3),抛物线的顶点在第一象限,AB=4.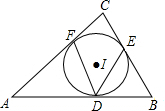 如图:⊙I内切于△ABC,切点分别为D、E、F,若∠A=50°,∠B=60°,连接DE,DE,则∠EDF=55°.
如图:⊙I内切于△ABC,切点分别为D、E、F,若∠A=50°,∠B=60°,连接DE,DE,则∠EDF=55°.