题目内容
17.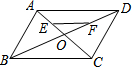 如图,在平行四边形ABCD中,AC与BD相交于点O,点E、F分别是OA、OD的中点,如果$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BO}$=$\overrightarrow{b}$,那么$\overrightarrow{EF}$=$\frac{1}{2}$$\overrightarrow{a}$+$\overrightarrow{b}$.
如图,在平行四边形ABCD中,AC与BD相交于点O,点E、F分别是OA、OD的中点,如果$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BO}$=$\overrightarrow{b}$,那么$\overrightarrow{EF}$=$\frac{1}{2}$$\overrightarrow{a}$+$\overrightarrow{b}$.
分析 根据平行四边形法则表示出$\overrightarrow{BC}$,再根据三角形的中位线平行于第三边并且等于第三边的一半求解即可.
解答 解:由向量的平行四边形法则得,$\overrightarrow{BA}$+$\overrightarrow{BC}$=2$\overrightarrow{BO}$,
所以,$\overrightarrow{BC}$=2$\overrightarrow{BO}$-$\overrightarrow{BA}$,
∵$\overrightarrow{AB}$=$\overrightarrow{a}$,
∴$\overrightarrow{BA}$=-$\overrightarrow{a}$,
∴$\overrightarrow{BC}$=2$\overrightarrow{b}$+$\overrightarrow{a}$,
∵点E、F分别是OA、OD的中点,
∴EF∥AD且EF=$\frac{1}{2}$AD,
∴EF∥BC且EF=$\frac{1}{2}$BC,
∴$\overrightarrow{EF}$=$\frac{1}{2}$$\overrightarrow{BC}$,
∴$\overrightarrow{EF}$=$\frac{1}{2}$$\overrightarrow{a}$+$\overrightarrow{b}$.
故答案为:$\frac{1}{2}$$\overrightarrow{a}$+$\overrightarrow{b}$.
点评 本题考查了平面向量,三角形的中位线平行于第三边并且等于第三边的一半,向量的问题,熟练掌握平行四边形法则和三角形法则是解题的关键,要注意方向.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案
相关题目
2.某人向东行走5米,记作“+5米”,那么他向西行走3米,记作( )
| A. | “-3米” | B. | “+3米” | C. | “-8米” | D. | “+8米” |
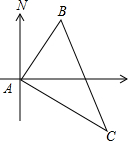 甲、乙两船同时从A码头开出,45分钟后,甲船到达B码头,乙船到达C码头,这时两船相距15海里;已知甲船航行的速度是12海里/时.乙船航行的速度是16海里/时,甲船航行的方向是北偏东40°,求乙船航行的方向.
甲、乙两船同时从A码头开出,45分钟后,甲船到达B码头,乙船到达C码头,这时两船相距15海里;已知甲船航行的速度是12海里/时.乙船航行的速度是16海里/时,甲船航行的方向是北偏东40°,求乙船航行的方向.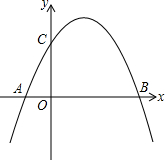 如图,抛物线y=-x2+bx+c与x轴交于AB两点(A在B的左侧),与y轴相交于点C(0,3),抛物线的顶点在第一象限,AB=4.
如图,抛物线y=-x2+bx+c与x轴交于AB两点(A在B的左侧),与y轴相交于点C(0,3),抛物线的顶点在第一象限,AB=4.