题目内容
15.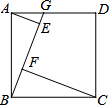 如图,G为正方形ABCD的边AD上的一个动点,AE⊥BG,CF⊥BG,垂足分别为点E,F.已知AD=4,则AE2+CF2=16.
如图,G为正方形ABCD的边AD上的一个动点,AE⊥BG,CF⊥BG,垂足分别为点E,F.已知AD=4,则AE2+CF2=16.
分析 只要证明△AEB≌△BFC,即可推出BE=CF,在Rt△AEB中,由AE2+BE2=AB2=16,即可解决问题.
解答 解: ∵四边形ABCD是正方形,
∵四边形ABCD是正方形,
∴AB=BC=AD=4,∠ABC=90°,
∵AE⊥BG,CF⊥BG,
∴∠AEB=∠CFB=90°,
∵∠ABE+∠CBF=90°,∠CBF+∠BCF=90°,
∴∠ABE=∠BCF,
在△ABE和△BCF中
$\left\{\begin{array}{l}{∠AEB=∠CFB}\\{∠ABE=∠BCF}\\{AB=BC}\end{array}\right.$,
∴△AEB≌△BFC,
∴BE=CF,
在Rt△AEB中,∵AE2+BE2=AB2=16,
∴AE2+CF2=16,
故答案为16.
点评 本题考查正方形的性质、全等三角形的判定和性质、勾股定理等知识,解题的关键是学会正确寻找全等三角形解决问题,属于中考常考题型.

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
5. 如图,把一块含有45°的直角三角形的两个顶点放在直尺的对边上.如果∠1=20°,那么∠2的度数是( )
如图,把一块含有45°的直角三角形的两个顶点放在直尺的对边上.如果∠1=20°,那么∠2的度数是( )
 如图,把一块含有45°的直角三角形的两个顶点放在直尺的对边上.如果∠1=20°,那么∠2的度数是( )
如图,把一块含有45°的直角三角形的两个顶点放在直尺的对边上.如果∠1=20°,那么∠2的度数是( )| A. | 15° | B. | 20° | C. | 30° | D. | 25° |
6.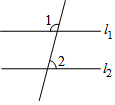 如图,l1∥l2,∠1=110°,则∠2的度数是( )
如图,l1∥l2,∠1=110°,则∠2的度数是( )
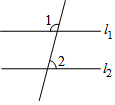 如图,l1∥l2,∠1=110°,则∠2的度数是( )
如图,l1∥l2,∠1=110°,则∠2的度数是( )| A. | 68° | B. | 70° | C. | 105° | D. | 110° |
4.不等式x≤3的最大整数解是( )
| A. | x=4 | B. | x=3 | C. | x=2 | D. | x=0 |
5.2016年国庆节期间,沈阳共接待游客约657.9万人次,657.9万用科学记数法表示为( )
| A. | 0.6579×103 | B. | 6.579×102 | C. | 6.579×106 | D. | 65.79×105 |
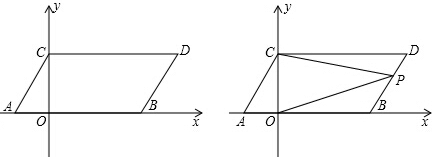
 三角板的直角顶点在直线a上,已知∠1=25°,则∠2的度数为65°.
三角板的直角顶点在直线a上,已知∠1=25°,则∠2的度数为65°.