题目内容
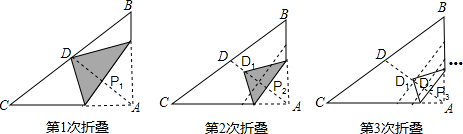
如图,直角三角形纸片ABC中,AB=3,AC=4,D为斜边BC中点,第1次将纸片折叠,使点A与点D重合,折痕与AD交于点P1;设P1D的中点为D1,第2次将纸片折叠,使点A与点D1重合,折痕与AD交于点P2;设P2D1的中点为D2,第3次将纸片折叠,使点A与点D2重合,折痕与AD交于点P3;…;则AP3的长为 .

考点:翻折变换(折叠问题)
专题:规律型
分析:如图,首先求出BC、AD的长度;借助翻折变换的性质求出AP1、AP2、AP3,即可解决问题.
解答: 解:由题意得:
解:由题意得:
BC=
=5;
∵点D为斜边上的中线
∴AD=
;由题意得:
AP1=
×
=
;
AP2=
(
+
×
)=
,
AP3=
(
+
×
)=
.
故答案为
.
 解:由题意得:
解:由题意得:BC=
| 32+42 |
∵点D为斜边上的中线
∴AD=
| 5 |
| 2 |
AP1=
| 5 |
| 2 |
| 1 |
| 2 |
| 5 |
| 4 |
AP2=
| 1 |
| 2 |
| 5 |
| 4 |
| 5 |
| 4 |
| 1 |
| 2 |
| 15 |
| 16 |
AP3=
| 1 |
| 2 |
| 15 |
| 16 |
| 15 |
| 16 |
| 1 |
| 2 |
| 45 |
| 64 |
故答案为
| 45 |
| 64 |
点评:该题主要考查了翻折变换的性质、勾股定理、直角三角形的性质等几何知识点及其应用问题;灵活运用翻折变换的性质,正确找出命题中隐含的数量关系是关键;对运算求解能力提出了较高的要求.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
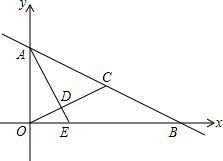 如图,在平面直角坐标系中,点A在y轴上,点B在x轴上,C是线段AB的中点,连接OC,并过点A作OC的垂线,垂足为D,交x轴于点E,已知tan∠OAD=
如图,在平面直角坐标系中,点A在y轴上,点B在x轴上,C是线段AB的中点,连接OC,并过点A作OC的垂线,垂足为D,交x轴于点E,已知tan∠OAD=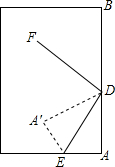 如图,斜折一页书的一角,使点A落在同一页书内的A′处,DE为折痕,作DF平分∠A′DB,试猜想∠FDE=
如图,斜折一页书的一角,使点A落在同一页书内的A′处,DE为折痕,作DF平分∠A′DB,试猜想∠FDE=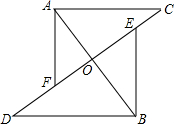 如图,线段AB、CD相交于点O,AC∥DB,AC∥DB,AO=BO,E、F分别为OC、OD的中点,连结AF、BE,求证:AF∥BE.
如图,线段AB、CD相交于点O,AC∥DB,AC∥DB,AO=BO,E、F分别为OC、OD的中点,连结AF、BE,求证:AF∥BE. 如图,将Rt△ABC沿某条直线折叠,使斜边的两个端点A与B重合,折痕为DE.AC=6,BC=8,∠CAE:∠BAE=1:2,
如图,将Rt△ABC沿某条直线折叠,使斜边的两个端点A与B重合,折痕为DE.AC=6,BC=8,∠CAE:∠BAE=1:2, 已知:如图,直线y=
已知:如图,直线y= 如图,在Rt△ABC中,∠C=90°,AC=4,cosA=
如图,在Rt△ABC中,∠C=90°,AC=4,cosA=