题目内容
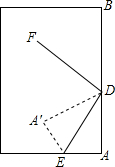 如图,斜折一页书的一角,使点A落在同一页书内的A′处,DE为折痕,作DF平分∠A′DB,试猜想∠FDE=
如图,斜折一页书的一角,使点A落在同一页书内的A′处,DE为折痕,作DF平分∠A′DB,试猜想∠FDE=考点:翻折变换(折叠问题)
专题:
分析:如图,首先证明∠ADE=∠A′DE(设为α);然后证明∠A′DF=∠BDF(设为β);求出α+β=90°,即可解决问题.
解答: 解:猜想:∠FDE=90°.理由如下:
解:猜想:∠FDE=90°.理由如下:
如图,由题意得:∠ADE=∠A′DE(设为α);
∵DF平分∠A′DB,
∴∠A′DF=∠BDF(设为β);
∵2(α+β)=180°,
∴α+β=90°,
∴∠FDE=90°.
故答案为90°.
 解:猜想:∠FDE=90°.理由如下:
解:猜想:∠FDE=90°.理由如下:如图,由题意得:∠ADE=∠A′DE(设为α);
∵DF平分∠A′DB,
∴∠A′DF=∠BDF(设为β);
∵2(α+β)=180°,
∴α+β=90°,
∴∠FDE=90°.
故答案为90°.
点评:该题考查了翻折变换的性质、角平分线的定义及其应用问题;牢固掌握翻折变换性质的本质是灵活运用、解题的基础和关键.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目
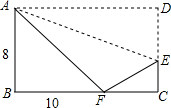 如图,在平面直角坐标系中放入一张长方形纸片ABCD,其中B是坐标原点,BC,AB分别在x轴、y轴的正半轴上,现将纸片沿AE翻折,使点D落在x轴上,记为F,若AB=8,BC=10,则E点的坐标为( )
如图,在平面直角坐标系中放入一张长方形纸片ABCD,其中B是坐标原点,BC,AB分别在x轴、y轴的正半轴上,现将纸片沿AE翻折,使点D落在x轴上,记为F,若AB=8,BC=10,则E点的坐标为( )| A、(10,4) |
| B、(10,3) |
| C、(6,4) |
| D、(6,3) |
下列4个命题:①矩形的对角线互相平分且相等;②对角线互相垂直的四边形是菱形;③等腰梯形的两条对角线相等;④等腰三角形底边上的中点到两腰的距离相等.其中正确的是( )
| A、①②③ | B、②③④ |
| C、①②④ | D、①③④ |

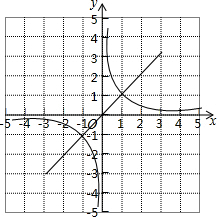 如图是函数y=x与y=
如图是函数y=x与y=