题目内容
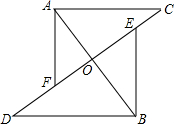 如图,线段AB、CD相交于点O,AC∥DB,AC∥DB,AO=BO,E、F分别为OC、OD的中点,连结AF、BE,求证:AF∥BE.
如图,线段AB、CD相交于点O,AC∥DB,AC∥DB,AO=BO,E、F分别为OC、OD的中点,连结AF、BE,求证:AF∥BE.考点:平行四边形的判定与性质,全等三角形的判定与性质
专题:证明题
分析:由AC∥BD,可得∠C=∠D,易证△AOC≌△BOD,从而得出OC=OD由E,F分别为OC,OD中点可得OE=OF,易得△AOF≌△BOE,可得出∠AFO=∠BEO利用同位角相等可得AF∥BE
解答:证明:∵AC∥BD,
∴∠C=∠D,
在△AOC和△BOD中,
,
∴△AOC≌△BOD(AAS)
∴OC=OD
∵E,F分别为OC,OD中点
∴OE=OF
在∴△AOF和△BOE中,
,
∴△AOF≌△BOE(SAS),
∴∠AFO=∠BEO,
∴AF∥BE.
∴∠C=∠D,
在△AOC和△BOD中,
|
∴△AOC≌△BOD(AAS)
∴OC=OD
∵E,F分别为OC,OD中点
∴OE=OF
在∴△AOF和△BOE中,
|
∴△AOF≌△BOE(SAS),
∴∠AFO=∠BEO,
∴AF∥BE.
点评:本题主要考查了全等三角形的判定与性质,解题的关键是证出△AOC≌△BOD.

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
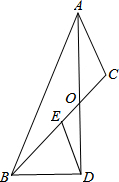 △ABC中,AO平分∠BAC,BD⊥AD,交AO延长线于点D,E为BC中点,求证:DE=
△ABC中,AO平分∠BAC,BD⊥AD,交AO延长线于点D,E为BC中点,求证:DE= 如图,把长方形纸片ABCD沿EF折叠后,使得点D与点B重合,点C落在点C′的位置上.
如图,把长方形纸片ABCD沿EF折叠后,使得点D与点B重合,点C落在点C′的位置上.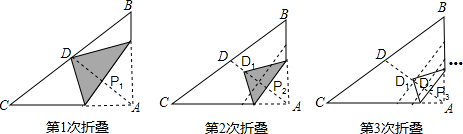
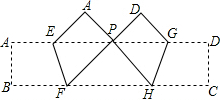 如图所示,折叠矩形纸条ABCD,使B,C两点落在AD边的P点处,折痕为EF,GH,若∠FPH的度数恰好为90°,PF=8,PH=6,则矩形ABCD的边BC的长为( )
如图所示,折叠矩形纸条ABCD,使B,C两点落在AD边的P点处,折痕为EF,GH,若∠FPH的度数恰好为90°,PF=8,PH=6,则矩形ABCD的边BC的长为( ) 如图,点A在双曲线y=
如图,点A在双曲线y=