题目内容
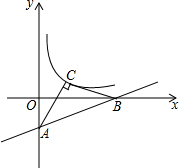 已知:如图,直线y=
已知:如图,直线y=| 1 |
| 5 |
| k |
| x |
考点:反比例函数与一次函数的交点问题
专题:
分析:先根据直线y=
x-1与坐标轴交于A、B两点求出两点坐标,再设C(x,y),由等腰三角形的性质可知AC=BC,过点C作CD⊥y轴于点D,则CD2+AD2=AC2,2AC2=AB2,故可得出关于x、y的关系式,求出x、y的值即可.
| 1 |
| 5 |
解答: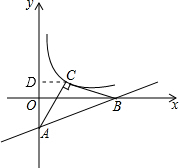 解:∵直线y=
解:∵直线y=
x-1交x轴于B,交y轴于A,
∴A(0,-1),B(5,0).
设C(x,y),
∵△ABC为等腰直角三角形,
∴AC=BC,即x2+(y+1)2=(5-x)2+y2 ①,
过点C作CD⊥y轴于点D,
∵CD2+AD2=AC2,2AC2=AB2,即x2+(y+1)2=AC2,2AC2=26,
∴2x2+2(y+1)2=26②,
①②联立得,
,
解得x=2或3,
由①得,y=12-5x,
当x=2时,y=12-5×2=2,
当x=3时,x=12-5×3=-3(舍去);
∴C(2,2),
∵点C在反比例函数y=
上,
∴k=2×2=4.
 解:∵直线y=
解:∵直线y=| 1 |
| 5 |
∴A(0,-1),B(5,0).
设C(x,y),
∵△ABC为等腰直角三角形,
∴AC=BC,即x2+(y+1)2=(5-x)2+y2 ①,
过点C作CD⊥y轴于点D,
∵CD2+AD2=AC2,2AC2=AB2,即x2+(y+1)2=AC2,2AC2=26,
∴2x2+2(y+1)2=26②,
①②联立得,
|
解得x=2或3,
由①得,y=12-5x,
当x=2时,y=12-5×2=2,
当x=3时,x=12-5×3=-3(舍去);
∴C(2,2),
∵点C在反比例函数y=
| k |
| x |
∴k=2×2=4.
点评:本题考查的是反比例函数与一次函数的交点问题,等腰直角三角形的性质及两点间的距离公式、勾股定理、反比例函数的性质,根据题意作出辅助线,列出关于x、y的方程组是解答此题的关键.

练习册系列答案
相关题目
用配方法解一元二次方程x2+4x-5=0,此方程可变形为( )
| A、(x-2)2=9 |
| B、(x+2)2=9 |
| C、(x+2)2=1 |
| D、(x-2)2=1 |
 如图,点A在双曲线y=
如图,点A在双曲线y=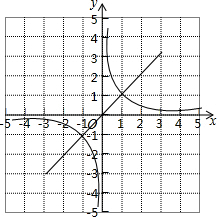 如图是函数y=x与y=
如图是函数y=x与y=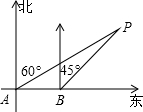 如图,海上有一灯塔P,在它周围15海里处有暗礁,一艘客轮以18海里/时的速度由西向东航行,行至A点处测得P在它的北偏东60°的方向,继续行驶40分钟后,到达B处又测得灯塔P在它的北偏东45°方向,问客轮不改变方向继续前进有无触礁的危险?(参考数据
如图,海上有一灯塔P,在它周围15海里处有暗礁,一艘客轮以18海里/时的速度由西向东航行,行至A点处测得P在它的北偏东60°的方向,继续行驶40分钟后,到达B处又测得灯塔P在它的北偏东45°方向,问客轮不改变方向继续前进有无触礁的危险?(参考数据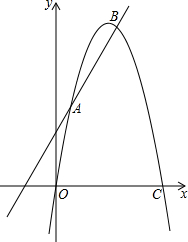 如图所示,已知抛物线y=ax2+bx+c与直线y=kx+4相交于A(1,5),B(4,8)两点,与x轴交于原点O及C点.
如图所示,已知抛物线y=ax2+bx+c与直线y=kx+4相交于A(1,5),B(4,8)两点,与x轴交于原点O及C点.