题目内容
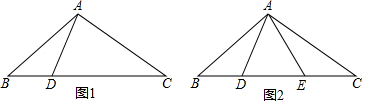
9．已知：如图，在△ABC中，AB=AC，∠BAC=120°，DA⊥AC．（1）求证：BD=AD；
（2）取DC的中点E，连接AE，请确定线段AD与BC的数量关系，并说明理由．
分析 （1）根据等腰三角形的性质得到∠B=∠C=30°，根据垂直的定义得到∠DAC=90°，得到∠BAD=30°，根据等腰三角形的判定即可得到结论；
（2）根据直角三角形的性质即可得到结论．
解答 解：（1）∵AB=AC，∠BAC=120°，
∴∠B=∠C=30°，
∵DA⊥AC，
∴∠DAC=90°，
∴∠BAD=30°，
∴∠B=∠BAD，
∴BD=AD；
（2）AD=$\frac{1}{3}$BC，
理由：∵∠DAC=90°，∠C=30°，
∴CD=2AD，
∵AD=BD，
∴AD=$\frac{1}{3}$BC．
点评 本题考查了等腰三角形的性质，含30°直角三角形的性质，熟练掌握等腰三角形的性质是解题的关键．
练习册系列答案
黄冈小状元解决问题天天练系列答案
相关题目
如图是一个正方体的展开图，标注了字母A的面是正方体的正面，如果正方体的左面和右面所标注代数式的值相等，则x的值是5或-1．