题目内容
15.从-1,0,1,3,4五个数中,随机抽取一个数记为a,那么使一次函数y=-3x+a不经过第三象限,且使关于x的分式方程$\frac{1-ax}{x-2}+2=\frac{1}{2-x}$有整数解的概率是$\frac{3}{5}$.分析 首先根据一次函数y=-3x+a不经过第三象限,可得a>0;然后根据分式方程的求解方法,求出关于x的分式方程$\frac{1-ax}{x-2}+2=\frac{1}{2-x}$的解是多少,进而判断出它有整数解时a的值是多少;最后确定出满足题意的a的数量,根据随机事件A的概率P(A)=事件A可能出现的结果数÷所有可能出现的结果数,用满足题意的a的数量除以5,求出概率为多少即可.
解答 解:∵一次函数y=-3x+a不经过第三象限,
∴a>0,
∵$\frac{1-ax}{x-2}+2=\frac{1}{2-x}$,
∴x=$\frac{2}{2-a}$,
∵关于x的分式方程$\frac{1-ax}{x-2}+2=\frac{1}{2-x}$有整数解,
∴a=0,1,3,4,
∵a=1时,x=2是增根,
∴a=0,3,4
综上,可得
满足题意的a的值有3个:1,3,4,
∴使一次函数y=-3x+a不经过第三象限,且使关于x的分式方程$\frac{1-ax}{x-2}+2=\frac{1}{2-x}$有整数解的概率是:
3÷5=$\frac{3}{5}$.
故答案为:$\frac{3}{5}$.
点评 (1)此题主要考查了概率公式的应用,要熟练掌握,解答此题的关键是要明确:随机事件A的概率P(A)=事件A可能出现的结果数÷所有可能出现的结果数.
(2)此题还考查了分式方程的求解问题,要注意:在解方程的过程中因为在把分式方程化为整式方程的过程中,扩大了未知数的取值范围,可能产生增根,增根是令分母等于0的值,不是原分式方程的解.
(3)此题还考查了一次函数的图象与系数的关系,要熟练掌握,解答此题的关键是要明确:①k>0,b>0?y=kx+b的图象在一、二、三象限;②k>0,b<0?y=kx+b的图象在一、三、四象限;③k<0,b>0?y=kx+b的图象在一、二、四象限;④k<0,b<0?y=kx+b的图象在二、三、四象限.

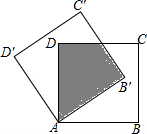 如图,将正方形纸片ABCD绕着点A按逆时针方向旋转30°后得到正方形AB′C′D′,若AB=2$\sqrt{3}$cm,则图中阴影部分的面积为( )
如图,将正方形纸片ABCD绕着点A按逆时针方向旋转30°后得到正方形AB′C′D′,若AB=2$\sqrt{3}$cm,则图中阴影部分的面积为( )| A. | 6cm2 | B. | (12-6$\sqrt{3}$)cm2 | C. | 3$\sqrt{3}$cm2 | D. | 4$\sqrt{3}$cm2 |
| A. | 某班45位同学,其中有2位同学生日相同 | |
| B. | 在装只有10个红球的布袋中摸出一球,这球一定是红球 | |
| C. | 今天是星期五,明天就是星期日 | |
| D. | 同号两个实数的积一定是正数 |
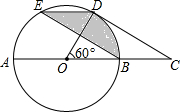 如图,在⊙O中,AB是直径,点D是⊙O上一点且∠BOD=60°,过点D作⊙O的切线CD交AB的延长线于点C,E为$\widehat{AD}$的中点,连接DE,EB.
如图,在⊙O中,AB是直径,点D是⊙O上一点且∠BOD=60°,过点D作⊙O的切线CD交AB的延长线于点C,E为$\widehat{AD}$的中点,连接DE,EB. 某校240名学生参加“献爱心”义务捐款活动.要求每人捐4-7元,(捐款数
某校240名学生参加“献爱心”义务捐款活动.要求每人捐4-7元,(捐款数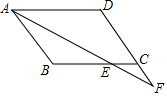 如图,在四边形ABCD中,AB∥CD,∠BAD的平分线交直线BC于点E,交直线DC于点F,若CE=CF,求证:四边形ABCD是平行四边形.
如图,在四边形ABCD中,AB∥CD,∠BAD的平分线交直线BC于点E,交直线DC于点F,若CE=CF,求证:四边形ABCD是平行四边形.