题目内容
5.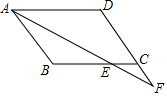 如图,在四边形ABCD中,AB∥CD,∠BAD的平分线交直线BC于点E,交直线DC于点F,若CE=CF,求证:四边形ABCD是平行四边形.
如图,在四边形ABCD中,AB∥CD,∠BAD的平分线交直线BC于点E,交直线DC于点F,若CE=CF,求证:四边形ABCD是平行四边形.
分析 根据角平分线的性质可得∠1=∠2,再根据平行线的性质可得∠1=∠F,由CE=CF,可得∠F=∠3,再利用等量代换可得∠2=∠3,进而可得判定AD∥BC,然后可得四边形ABCD是平行四边形.
解答  证明:∵∠BAD的平分线交直线BC于点E,
证明:∵∠BAD的平分线交直线BC于点E,
∴∠1=∠2,
∵AB∥CD,
∴∠1=∠F,
∵CE=CF,
∴∠F=∠3,
∴∠1=∠3,
∴∠2=∠3,
∴AD∥BC,
∵AB∥CD,
∴四边形ABCD是平行四边形.
点评 此题主要考查了平行四边形的判定,关键是掌握两组对边分别平行的四边形是平行四边形.

练习册系列答案
 同步奥数系列答案
同步奥数系列答案
相关题目
16.两个实根之和为3的一元二次方程是( )
| A. | 2x2-3x+1=0 | B. | x2+1=3x | C. | x2-3x+4=0 | D. | 3x2+9x-1=0 |
13.下列图形中,不是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
17.在今年的中招体育考试中,我校甲、乙、丙、丁四个班级的平均分完全一样,方差分别为:S甲2=8.5,S乙2=21.7,S丙2=15,S丁2=17.2,则四个班体考成绩最稳定的是( )
| A. | 甲班 | B. | 乙班 | C. | 丙班 | D. | 丁班 |
15.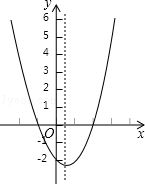 二次函数y=ax2+bx+c(a≠0)的大致图象如图,关于该二次函数,下列说法错误的是( )
二次函数y=ax2+bx+c(a≠0)的大致图象如图,关于该二次函数,下列说法错误的是( )
 二次函数y=ax2+bx+c(a≠0)的大致图象如图,关于该二次函数,下列说法错误的是( )
二次函数y=ax2+bx+c(a≠0)的大致图象如图,关于该二次函数,下列说法错误的是( )| A. | 函数有最小值 | B. | 对称轴是直线x=$\frac{1}{2}$ | ||
| C. | 当-1<x<2时,y>0 | D. | 当x<$\frac{1}{2}$,y随x的增大而减小 |
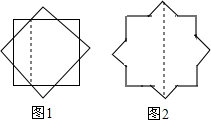 如图2的正八角形是由两个正方形(如图1)中的一个正方形绕着它的中心顺时针旋转45°形成的.
如图2的正八角形是由两个正方形(如图1)中的一个正方形绕着它的中心顺时针旋转45°形成的.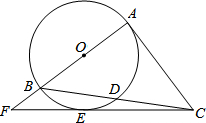 如图,Rt△ABC中,∠A=90°,以AB为直径的⊙O交BC于点D,点E在⊙O上,CE=CA,AB,CE的延长线交于点F.
如图,Rt△ABC中,∠A=90°,以AB为直径的⊙O交BC于点D,点E在⊙O上,CE=CA,AB,CE的延长线交于点F.