题目内容
6.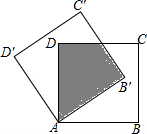 如图,将正方形纸片ABCD绕着点A按逆时针方向旋转30°后得到正方形AB′C′D′,若AB=2$\sqrt{3}$cm,则图中阴影部分的面积为( )
如图,将正方形纸片ABCD绕着点A按逆时针方向旋转30°后得到正方形AB′C′D′,若AB=2$\sqrt{3}$cm,则图中阴影部分的面积为( )| A. | 6cm2 | B. | (12-6$\sqrt{3}$)cm2 | C. | 3$\sqrt{3}$cm2 | D. | 4$\sqrt{3}$cm2 |
分析 设CD,B′C′相交于点M,DM=x,则∠MAD=30°,AM=2x,x2+(2$\sqrt{3}$)2=4x2,解得x=2,所以重叠部分的面积SADMB′=2S△ADM.
解答 解:设CD,B′C′相交于点M,DM=x,则∠MAD=30° AM=2x,
∵x2++(2$\sqrt{3}$)2=4x2,
∴x=2,
∴S△ADM=$\frac{1}{2}$•AD•DM=$\frac{1}{2}$×2$\sqrt{3}$×2=2$\sqrt{3}$,
∴重叠部分的面积SADMB′=4$\sqrt{3}$.
故选:D.
点评 本题考查旋转的性质.旋转变化前后,对应点到旋转中心的距离相等以及每一对对应点与旋转中心连线所构成的旋转角相等.要注意旋转的三要素:①定点-旋转中心;②旋转方向;③旋转角度.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
14.已知平行四边形ABCD的对角钱AC与BD相交于点O,AB⊥AC,若AB=2,AC=8,则对角线BD的长是( )
| A. | 2$\sqrt{2}$ | B. | 2$\sqrt{5}$ | C. | 4$\sqrt{2}$ | D. | 4$\sqrt{5}$ |
1.某校初一年级为了解学生课堂发言情况,随机抽取该年级部分学生,对他们某天在课堂上发言的次数进行了统计,其结果如下表,并绘制了如图所示的两幅不完整的统计图,已知B、E两组发言人数的比为5;2,请结合图中相关数据回答下列问题:

(1)求出样本容量,并补全直方图(在图中标出各组人数);
(2)课堂发言次数的中位数落在哪个组;
(3)该年级共有学生500人,请估计全年级在这天里发言次数不少于12次的人数.

(1)求出样本容量,并补全直方图(在图中标出各组人数);
(2)课堂发言次数的中位数落在哪个组;
(3)该年级共有学生500人,请估计全年级在这天里发言次数不少于12次的人数.
| 组别 | 课堂发言次数n |
| A | 0≤n<3 |
| B | 3≤n<6 |
| C | 6≤n<9 |
| D | 9≤n<12 |
| E | 12≤n<15 |
| F | 15≤n<18 |
16.两个实根之和为3的一元二次方程是( )
| A. | 2x2-3x+1=0 | B. | x2+1=3x | C. | x2-3x+4=0 | D. | 3x2+9x-1=0 |
 如图,一只蚂蚁沿着棱长为2的正方体表面从点A出发,经过3个面爬到点B,如果它运动的路径是最短的,则AC的长为$\frac{2\sqrt{10}}{3}$.
如图,一只蚂蚁沿着棱长为2的正方体表面从点A出发,经过3个面爬到点B,如果它运动的路径是最短的,则AC的长为$\frac{2\sqrt{10}}{3}$.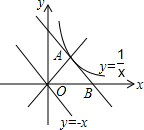 如图,函数y=-x的图象是二、四象限的角平分线,将y=-x的图象以点O为中心旋转90°与函数y=$\frac{1}{x}$的图象交于点A,再将y=-x的图象向右平移至点A,与x轴交于点B,则点B的坐标为(2,0).
如图,函数y=-x的图象是二、四象限的角平分线,将y=-x的图象以点O为中心旋转90°与函数y=$\frac{1}{x}$的图象交于点A,再将y=-x的图象向右平移至点A,与x轴交于点B,则点B的坐标为(2,0). 如图,将Rt△ABC绕直角顶点顺时针旋转90°,得到△A′B′C,连接AA′,∠1=26°,则∠B的度数是71°.
如图,将Rt△ABC绕直角顶点顺时针旋转90°,得到△A′B′C,连接AA′,∠1=26°,则∠B的度数是71°.