题目内容
20. 如图,AB长为2$\sqrt{3}$,BC长为4,AF长为10,求正方形CDEF的周长.
如图,AB长为2$\sqrt{3}$,BC长为4,AF长为10,求正方形CDEF的周长.
分析 在直角△ABC中,根据勾股定理即可求得AC2,然后在直角△ACF中求得FC,根据正方形CDEF的周长=4FC即可求解.
解答 解:在直角△ABC中,AC2=AB2+BC2=(2$\sqrt{3}$)2+42=28,
在直角△ACF中,FC2=AF2+AC2=102+28=128.
∴CF=8$\sqrt{2}$,
而正方形CDEF的周长=4CF=32$\sqrt{2}$.
点评 本题主要考查了正方形的性质,勾股定理,正确理解图形中几个直角三角形与正方形的关系是解决本题的关键.

练习册系列答案
相关题目
15.有一块长为m,宽为n的长方形铝片,四角各截去一个相同的边长为x的小正方形,折起来做成一个没有盖的盒子,则此盒子的体积可表示为( )
| A. | x(m-x)(n-x) | B. | x2(m-x)(n-x) | C. | $\frac{1}{3}$x(m-2n)(n-2x) | D. | x(m-2x)(n-2x) |
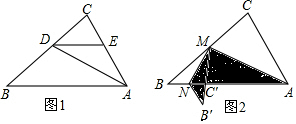
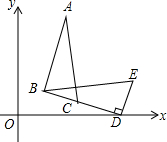 如图,在△BDE中,∠BDE=90°,BD=3$\sqrt{2}$,点D的坐标是(5,0),∠BDO=15°,将△BDE旋转得到△ABC的位置,点C在BD上,则过A、B、D三点圆的圆心坐标为($\frac{7}{2}$,$\frac{3}{2}$$\sqrt{3}$).
如图,在△BDE中,∠BDE=90°,BD=3$\sqrt{2}$,点D的坐标是(5,0),∠BDO=15°,将△BDE旋转得到△ABC的位置,点C在BD上,则过A、B、D三点圆的圆心坐标为($\frac{7}{2}$,$\frac{3}{2}$$\sqrt{3}$).