题目内容
19.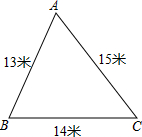 学校校内有一块如图所示的三角形空地ABC,计划将这块空地建成一个花园,以美化校园环境,预计花园每平方米造价为30元,学校修建这个花园需要投资多少元?
学校校内有一块如图所示的三角形空地ABC,计划将这块空地建成一个花园,以美化校园环境,预计花园每平方米造价为30元,学校修建这个花园需要投资多少元?
分析 过点D作AD⊥BC于点D,设BD=x,则CD=14-x,再根据勾股定理求出x的值,进而可得出AD的长,由三角形的面积公式即可得出结论.
解答  解:过点D作AD⊥BC于点D,设BD=x,则CD=14-x,
解:过点D作AD⊥BC于点D,设BD=x,则CD=14-x,
在Rt△ABD与Rt△ACD中,
∵AD2=AB2-BD2,AD2=AC2-CD2,
∴AB2-BD2=AC2-CD2,即132-x2=152-(14-x)2,解得x=5,
∴AD2=AB2-BD2=132-52=144,
∴AD=12(米),
∴学校修建这个花园的费用=30×$\frac{1}{2}$×14×12=2520(元).
答:学校修建这个花园需要投资2520元.
点评 本题考查的是勾股定理的应用及三角形的面积公式,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
7.甲、乙两名射击运动员在某次训练中各射击10发子弹,成绩如表:
且${\overline x_乙}$=8,S乙2=1.8,S甲2=1.2,根据上述信息完成下列问题:
(1)乙运动员射击训练成绩的众数是7,中位数是7.5.
(2)求甲运动员射击成绩的平均数,并判断甲、乙两人在本次射击成绩的稳定性.
| 甲 | 8 | 9 | 7 | 9 | 8 | 6 | 7 | 8 | 10 | 8 |
| 乙 | 6 | 7 | 9 | 7 | 9 | 10 | 8 | 7 | 7 | 10 |
(1)乙运动员射击训练成绩的众数是7,中位数是7.5.
(2)求甲运动员射击成绩的平均数,并判断甲、乙两人在本次射击成绩的稳定性.
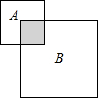 如图所示,在桌面上放着A、B两个正方形,共遮住的面积为21cm2.若这两个正方形折叠部分(阴影部分)的面积为3cm2,且正方形B除重叠部分外的面积是正方形A除重叠部分外的面积的2倍,则正方形A的面积是9cm2.
如图所示,在桌面上放着A、B两个正方形,共遮住的面积为21cm2.若这两个正方形折叠部分(阴影部分)的面积为3cm2,且正方形B除重叠部分外的面积是正方形A除重叠部分外的面积的2倍,则正方形A的面积是9cm2.
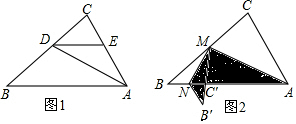
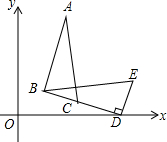 如图,在△BDE中,∠BDE=90°,BD=3$\sqrt{2}$,点D的坐标是(5,0),∠BDO=15°,将△BDE旋转得到△ABC的位置,点C在BD上,则过A、B、D三点圆的圆心坐标为($\frac{7}{2}$,$\frac{3}{2}$$\sqrt{3}$).
如图,在△BDE中,∠BDE=90°,BD=3$\sqrt{2}$,点D的坐标是(5,0),∠BDO=15°,将△BDE旋转得到△ABC的位置,点C在BD上,则过A、B、D三点圆的圆心坐标为($\frac{7}{2}$,$\frac{3}{2}$$\sqrt{3}$).