题目内容
16.化简二次根式(x2-1)$\sqrt{-\frac{1}{1+x}}$,得出的结果是-(x-1)$\sqrt{-x-1}$.分析 原式利用二次根式性质化简,整理即可得到结果.
解答 解:原式=(x+1)(x-1)$\sqrt{-\frac{1+x}{(1+x)^{2}}}$=$\frac{(x+1)(x-1)}{|1+x|}$$\sqrt{-(1+x)}$=-(x-1)$\sqrt{-x-1}$,
故答案为:-(x-1)$\sqrt{-x-1}$
点评 此题考查了二次根式的性质与化简,以及绝对值的代数意义,熟练掌握运算法则是解本题的关键.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
4.抛物线y=-2(x-1)2-3与y轴交点的横坐标为( )
| A. | -3 | B. | -4 | C. | -5 | D. | -1 |
1.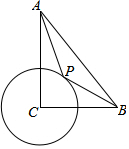 如图,在Rt△ABC中,∠ACB=90°,CB=4,CA=6,⊙C半径为2,P为圆上一动点,连结AP,BP,AP+$\frac{1}{2}$BP的最小值为( )
如图,在Rt△ABC中,∠ACB=90°,CB=4,CA=6,⊙C半径为2,P为圆上一动点,连结AP,BP,AP+$\frac{1}{2}$BP的最小值为( )
 如图,在Rt△ABC中,∠ACB=90°,CB=4,CA=6,⊙C半径为2,P为圆上一动点,连结AP,BP,AP+$\frac{1}{2}$BP的最小值为( )
如图,在Rt△ABC中,∠ACB=90°,CB=4,CA=6,⊙C半径为2,P为圆上一动点,连结AP,BP,AP+$\frac{1}{2}$BP的最小值为( )| A. | $\sqrt{37}$ | B. | 6 | C. | 2$\sqrt{17}$ | D. | 4 |
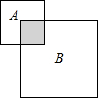 如图所示,在桌面上放着A、B两个正方形,共遮住的面积为21cm2.若这两个正方形折叠部分(阴影部分)的面积为3cm2,且正方形B除重叠部分外的面积是正方形A除重叠部分外的面积的2倍,则正方形A的面积是9cm2.
如图所示,在桌面上放着A、B两个正方形,共遮住的面积为21cm2.若这两个正方形折叠部分(阴影部分)的面积为3cm2,且正方形B除重叠部分外的面积是正方形A除重叠部分外的面积的2倍,则正方形A的面积是9cm2.
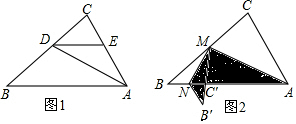
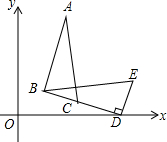 如图,在△BDE中,∠BDE=90°,BD=3$\sqrt{2}$,点D的坐标是(5,0),∠BDO=15°,将△BDE旋转得到△ABC的位置,点C在BD上,则过A、B、D三点圆的圆心坐标为($\frac{7}{2}$,$\frac{3}{2}$$\sqrt{3}$).
如图,在△BDE中,∠BDE=90°,BD=3$\sqrt{2}$,点D的坐标是(5,0),∠BDO=15°,将△BDE旋转得到△ABC的位置,点C在BD上,则过A、B、D三点圆的圆心坐标为($\frac{7}{2}$,$\frac{3}{2}$$\sqrt{3}$).