题目内容
20.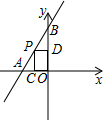 如图,一次函数y=2x+4的图象与x轴、y轴分别交于A、B两点,动点P在A、B之间运动(P与A、B不重合),过点P作PC⊥x轴,垂足为C,PD⊥y轴,垂足为D,问四边形OCPD的周长有可能为6吗?若能,求出点P的坐标;若不能,说明理由.
如图,一次函数y=2x+4的图象与x轴、y轴分别交于A、B两点,动点P在A、B之间运动(P与A、B不重合),过点P作PC⊥x轴,垂足为C,PD⊥y轴,垂足为D,问四边形OCPD的周长有可能为6吗?若能,求出点P的坐标;若不能,说明理由.
分析 根据一次函数图象上点的坐标特征可设点P的坐标为(m,2m+4)(-2<m<0),由此可得出PC、PD的长度,根据四边形OCPD的周长为6即可得出关于m的一元一次方程,解之即可得出m的值,再将其代入点P的坐标中即可.
解答 解:设点P的坐标为(m,2m+4)(-2<m<0),则PC=2m+4,PD=-m,
∵PC⊥x轴,PD⊥y轴,
∴四边形OCPD为矩形,
∴2(PC+PD)=2(2m+4-m)=6,
解得:m=-1,
∴四边形OCPD的周长可以为6,此时点P的坐标为(-1,3).
点评 本题考查了一次函数图象上点的坐标特征,根据四边形OCPD的周长为6列出关于m的一元一次方程是解题的关键.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
9.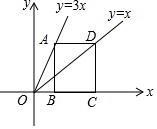 如图,点A、D分别在两条直线y=3x和y=x上,AD∥x轴,已知B、C都在x轴上,且四边形ABCD是矩形,则$\frac{AD}{AB}$的值是( )
如图,点A、D分别在两条直线y=3x和y=x上,AD∥x轴,已知B、C都在x轴上,且四边形ABCD是矩形,则$\frac{AD}{AB}$的值是( )
 如图,点A、D分别在两条直线y=3x和y=x上,AD∥x轴,已知B、C都在x轴上,且四边形ABCD是矩形,则$\frac{AD}{AB}$的值是( )
如图,点A、D分别在两条直线y=3x和y=x上,AD∥x轴,已知B、C都在x轴上,且四边形ABCD是矩形,则$\frac{AD}{AB}$的值是( )| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | 3 | D. | $\frac{3}{2}$ |



