题目内容
9.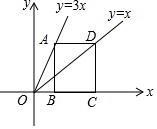 如图,点A、D分别在两条直线y=3x和y=x上,AD∥x轴,已知B、C都在x轴上,且四边形ABCD是矩形,则$\frac{AD}{AB}$的值是( )
如图,点A、D分别在两条直线y=3x和y=x上,AD∥x轴,已知B、C都在x轴上,且四边形ABCD是矩形,则$\frac{AD}{AB}$的值是( )| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | 3 | D. | $\frac{3}{2}$ |
分析 设点A的坐标为(m,3m),根据矩形的性质结合一次函数图象上点的坐标特征可得出点B、C、D的坐标,进而可得出AD、AB的长度,将其代入$\frac{AD}{AB}$中,即可得出结论.
解答 解:设点A的坐标为(m,3m),则点B的坐标为(m,0),点C的坐标为(3m,0),点D的坐标为(3m,3m),
∴AD=3m-m=2m,AB=3m,
∴$\frac{AD}{AB}$=$\frac{2m}{3m}$=$\frac{2}{3}$.
故选B.
点评 本题考查了一次函数图象上点的坐标特征以及矩形的性质,设出点A的坐标,利用矩形的性质结合一次函数图象上点的坐标特征表示出点B、C、D的坐标是解题的关键.

练习册系列答案
相关题目
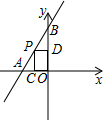 如图,一次函数y=2x+4的图象与x轴、y轴分别交于A、B两点,动点P在A、B之间运动(P与A、B不重合),过点P作PC⊥x轴,垂足为C,PD⊥y轴,垂足为D,问四边形OCPD的周长有可能为6吗?若能,求出点P的坐标;若不能,说明理由.
如图,一次函数y=2x+4的图象与x轴、y轴分别交于A、B两点,动点P在A、B之间运动(P与A、B不重合),过点P作PC⊥x轴,垂足为C,PD⊥y轴,垂足为D,问四边形OCPD的周长有可能为6吗?若能,求出点P的坐标;若不能,说明理由.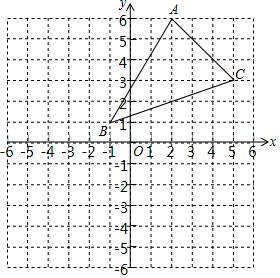 如图,三角形ABC经过平移后,使得点A与点A′(m,5)重合,使得点B与点B′(-5,n)重合.
如图,三角形ABC经过平移后,使得点A与点A′(m,5)重合,使得点B与点B′(-5,n)重合.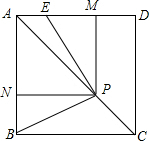 如图,已知正方形ABCD,P是对角线AC上任意一点,E为AD上的点,且∠EPB=90°,PM⊥AD,PN⊥AB.
如图,已知正方形ABCD,P是对角线AC上任意一点,E为AD上的点,且∠EPB=90°,PM⊥AD,PN⊥AB.