题目内容
10.(1)计算:(1-$\sqrt{3}$)2(1-$\sqrt{2}$)2(1+$\sqrt{2}$)2(1+$\sqrt{3}$)2-($\sqrt{3}$-$\sqrt{2}$)2(2)用适当方法解方程.x2-2x=2x+1.
分析 (1)根据平方差公式、完全平方公式、二次根式的加减法则计算;
(2)先把方程变形,利用公式法解出方程.
解答 解:(1)原式=[(1-$\sqrt{3}$)(1$+\sqrt{3}$)]2[(1-$\sqrt{2}$)(1$+\sqrt{2}$)]2-($\sqrt{3}$-$\sqrt{2}$)2
=4-3+2$\sqrt{6}$-2
=2$\sqrt{6}$-1;
(2)原方程变形为:x2-4x-1=0,
x=$\frac{4±\sqrt{20}}{2}$,
x1=2$+\sqrt{5}$,x2=2-$\sqrt{5}$.
点评 本题考查的是二次根式的混合运算、一元二次方程的解法,掌握平方差公式、二次根式的加减、公式法解一元二次方程的一般步骤是解题的关键.

练习册系列答案
相关题目
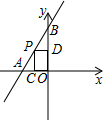 如图,一次函数y=2x+4的图象与x轴、y轴分别交于A、B两点,动点P在A、B之间运动(P与A、B不重合),过点P作PC⊥x轴,垂足为C,PD⊥y轴,垂足为D,问四边形OCPD的周长有可能为6吗?若能,求出点P的坐标;若不能,说明理由.
如图,一次函数y=2x+4的图象与x轴、y轴分别交于A、B两点,动点P在A、B之间运动(P与A、B不重合),过点P作PC⊥x轴,垂足为C,PD⊥y轴,垂足为D,问四边形OCPD的周长有可能为6吗?若能,求出点P的坐标;若不能,说明理由.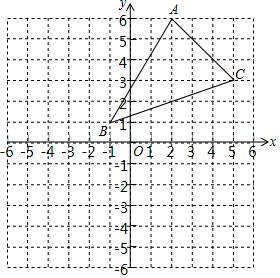 如图,三角形ABC经过平移后,使得点A与点A′(m,5)重合,使得点B与点B′(-5,n)重合.
如图,三角形ABC经过平移后,使得点A与点A′(m,5)重合,使得点B与点B′(-5,n)重合. 如图,由若干个棱长相同的小正方体堆成的几何体,请画出从正面、左面、上面看到的几何体的形状图.
如图,由若干个棱长相同的小正方体堆成的几何体,请画出从正面、左面、上面看到的几何体的形状图.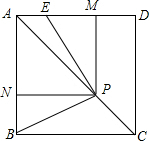 如图,已知正方形ABCD,P是对角线AC上任意一点,E为AD上的点,且∠EPB=90°,PM⊥AD,PN⊥AB.
如图,已知正方形ABCD,P是对角线AC上任意一点,E为AD上的点,且∠EPB=90°,PM⊥AD,PN⊥AB.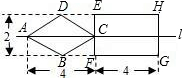 如图,直线l是菱形ABCD和矩形EFGH的对称轴,点C在EF边上,若菱形ABCD沿直线l从左向右匀速运动直至点C落在GH边上停止运动.能反映菱形进入矩形内部的周长y与运动的时间x之间关系的图象大致是( )
如图,直线l是菱形ABCD和矩形EFGH的对称轴,点C在EF边上,若菱形ABCD沿直线l从左向右匀速运动直至点C落在GH边上停止运动.能反映菱形进入矩形内部的周长y与运动的时间x之间关系的图象大致是( )