题目内容
5.在直角坐标系中,点P(a,b)的“变换点”P1的坐标定义如下:当a≥b时,点P1的坐标为(a,b);当a<b时,点P1的坐标为(b,a).依此定义,直线y=-2x+6上所有点的交换点组成一个新的图形L,直线y=kx+1与图形L有且只有一个公共点,则k的取值或取值范围是k=$\frac{1}{2}$或-2≤k<-$\frac{1}{2}$.分析 通过解不等式x≥-2x+6,可求出新的图形L的函数解析式,依照题意画出图形,并找出直线y=kx+1与图形L有且只有一个公共点的临界点,结合图形即可得出结论.
解答 解:令x≥-2x+6,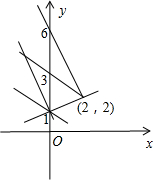
解得:x≥2,
∴新的图形L的函数解析式为y=$\left\{\begin{array}{l}{-2x+6(x≥2)}\\{-\frac{1}{2}x+3(x<2)}\end{array}\right.$.
当x=2时,y=-2x+6=2,
∴新图形L的拐点坐标为(2,2),画出图形如图所示.
当y=kx+1过点(2,2)时,有2=2k+1,
解得:k=$\frac{1}{2}$;
当y=kx+1与y=-2x+6平行时,k=-2;
当y=kx+1与y=-$\frac{1}{2}$x+3平行时,k=-$\frac{1}{2}$.
结合图形可知:直线y=kx+1与图形L有且只有一个公共点时,k=$\frac{1}{2}$或-2≤k<-$\frac{1}{2}$.
故答案为:k=$\frac{1}{2}$或-2≤k<-$\frac{1}{2}$.
点评 本题考查了一次函数图象上点的坐标特征、平行线的性质以及一次函数图象,依照题意画出图形,利用数形结合解决问题是解题的关键.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
4.下列运算正确的是( )
| A. | (2a2)2=2a4 | B. | 6a8÷3a2=2a4 | C. | 2a2•a=2a3 | D. | 3a2-2a2=1 |
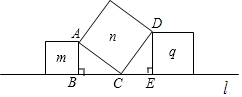
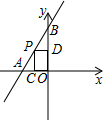 如图,一次函数y=2x+4的图象与x轴、y轴分别交于A、B两点,动点P在A、B之间运动(P与A、B不重合),过点P作PC⊥x轴,垂足为C,PD⊥y轴,垂足为D,问四边形OCPD的周长有可能为6吗?若能,求出点P的坐标;若不能,说明理由.
如图,一次函数y=2x+4的图象与x轴、y轴分别交于A、B两点,动点P在A、B之间运动(P与A、B不重合),过点P作PC⊥x轴,垂足为C,PD⊥y轴,垂足为D,问四边形OCPD的周长有可能为6吗?若能,求出点P的坐标;若不能,说明理由.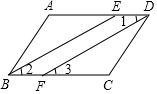 如图,在?ABCD中,BE,DF分别平分∠ABC,∠ADC.求证:BE∥DF.
如图,在?ABCD中,BE,DF分别平分∠ABC,∠ADC.求证:BE∥DF.