题目内容
2.已知M=x2-x-3,N=2x2-3x-1.(1)当N=2M时,求x的值;
(2)比较M与N的大小;
(3)当M=1时,求N•x-6M•x+2014的值.
分析 (1)直接根据N=2M建立关于x的方程,进而得解;
(2)用N减去M,再进行配方即可得解;
(3)根据M=1,求出x的值,再求出N的值,进而得解.
解答 解:(1)根据题意,得:2x2-3x-1=2(x2-x-3)
解得:x=5;
(2)N-M=2x2-3x-1-(x2-x-3)
=x2-2x+2
=(x-1)2+1>0,
∴N>M;
(3)当M=1时,x2-x-3=1,
∴x2=x+4,
∴N=2(x+4)-3x-1=-x+7,
∴N•x-6M•x+2014=(-x+7)x-6x+2014
=-x2+x+2014
=-(x+4)+x+2014
=-x-4+x+2014
=2010.
点评 本题主要考查了整式的混合运算,以及化简求值的问题,还考查了一元一次方程的解法,配方法等知识点,有一定的综合性,要注意认真总结.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
17.下列结论正确的是( )
| A. | 同位角相等 | |
| B. | 垂直于同一直线的两条直线互相平行 | |
| C. | 过一点有且只有一条直线与这条直线平行 | |
| D. | 同一平面内,不相交的两条直线叫做平行线 |
7. 如图,在?ABCD中,AB=6,AD=8,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE于G,BG=4$\sqrt{2}$,则四边形AECD的周长为( )
如图,在?ABCD中,AB=6,AD=8,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE于G,BG=4$\sqrt{2}$,则四边形AECD的周长为( )
 如图,在?ABCD中,AB=6,AD=8,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE于G,BG=4$\sqrt{2}$,则四边形AECD的周长为( )
如图,在?ABCD中,AB=6,AD=8,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE于G,BG=4$\sqrt{2}$,则四边形AECD的周长为( )| A. | 20 | B. | 21 | C. | 22 | D. | 23 |
11. 南水北调工程中线已经在12月27日开始向北京、天津等地供水.为了进一步加强居民的节水意识,合理调配水资源,某区决定对本区的居民用水实行额定用水管理.为了更好的确定额定用水的用水量,首先对本区居民的目前生活用水量进行了入户调查.下表是通过简单随机抽样获得的50个家庭去年的月均用水量(单位:吨).
南水北调工程中线已经在12月27日开始向北京、天津等地供水.为了进一步加强居民的节水意识,合理调配水资源,某区决定对本区的居民用水实行额定用水管理.为了更好的确定额定用水的用水量,首先对本区居民的目前生活用水量进行了入户调查.下表是通过简单随机抽样获得的50个家庭去年的月均用水量(单位:吨).
4.7 2.1 3.1 2.3 5.2 2.8 7.3 4.3 4.8 6.7
4.5 5.1 6.5 8.9 2.2 4.5 3.2 3.2 4.5 3.5
3.5 3.5 3.6 4.9 3.7 3.8 5.6 5.5 5.9 6.2
5.7 3.9 4.0 4.0 7.0 3.7 9.5 4.2 6.4 3.5
4.5 4.5 4.6 5.4 5.6 6.6 5.8 4.5 6.2 7.5
(1)请你将调查数据进行如下整理:
频数分布表
(2)结合整理的数据完成频数分布直方图,通过观察直方图你可以得到哪些信息?请你写出你得到的信息.
(3)为了鼓励节约用水,要确定一个用水量的标准,超出这个标准的部分按1.5倍价格收费.若要使60%的家庭收费不受影响,你觉得家庭月均用水量应该定多少吨?
 南水北调工程中线已经在12月27日开始向北京、天津等地供水.为了进一步加强居民的节水意识,合理调配水资源,某区决定对本区的居民用水实行额定用水管理.为了更好的确定额定用水的用水量,首先对本区居民的目前生活用水量进行了入户调查.下表是通过简单随机抽样获得的50个家庭去年的月均用水量(单位:吨).
南水北调工程中线已经在12月27日开始向北京、天津等地供水.为了进一步加强居民的节水意识,合理调配水资源,某区决定对本区的居民用水实行额定用水管理.为了更好的确定额定用水的用水量,首先对本区居民的目前生活用水量进行了入户调查.下表是通过简单随机抽样获得的50个家庭去年的月均用水量(单位:吨).4.7 2.1 3.1 2.3 5.2 2.8 7.3 4.3 4.8 6.7
4.5 5.1 6.5 8.9 2.2 4.5 3.2 3.2 4.5 3.5
3.5 3.5 3.6 4.9 3.7 3.8 5.6 5.5 5.9 6.2
5.7 3.9 4.0 4.0 7.0 3.7 9.5 4.2 6.4 3.5
4.5 4.5 4.6 5.4 5.6 6.6 5.8 4.5 6.2 7.5
(1)请你将调查数据进行如下整理:
频数分布表
| 分组 | 划记(用正字划记) | 频数 |
| 2.0<x≤3.5 | ||
| 3.5<x≤5.0 | ||
| 5.0<x≤6.5 | ||
| 6.5<x≤8.0 | ||
| 8.0<x≤9.5 | ||
| 合计 |
(3)为了鼓励节约用水,要确定一个用水量的标准,超出这个标准的部分按1.5倍价格收费.若要使60%的家庭收费不受影响,你觉得家庭月均用水量应该定多少吨?
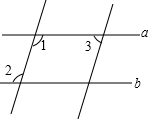 如图,已知直线a∥b,直线c∥d,∠1=107°,求∠2,∠3的度数.
如图,已知直线a∥b,直线c∥d,∠1=107°,求∠2,∠3的度数.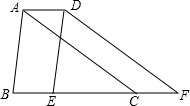 如图,将周长为18的三角形ABC向右平移2个单位后得到三角形DEF,则四边形ABFD的周长等于22.
如图,将周长为18的三角形ABC向右平移2个单位后得到三角形DEF,则四边形ABFD的周长等于22.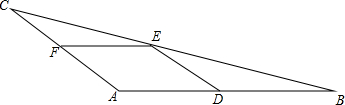 如图,△ABC中,D、E、F分别是AB、BC、AC上的点,四边形ADEF是菱形,AB=15,AC=10,则菱形的周长是( )
如图,△ABC中,D、E、F分别是AB、BC、AC上的点,四边形ADEF是菱形,AB=15,AC=10,则菱形的周长是( )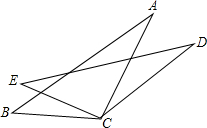 如图,AC=DC,BC=EC,∠ACD=∠BCE.求证:∠A=∠D.
如图,AC=DC,BC=EC,∠ACD=∠BCE.求证:∠A=∠D.