题目内容
14．
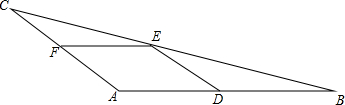如图，△ABC中，D、E、F分别是AB、BC、AC上的点，四边形ADEF是菱形，AB=15，AC=10，则菱形的周长是（ ）| A． | 6 | B． | 16 | C． | 24 | D． | 32 |
分析 首先设AD=x，由四边形ADEF是菱形，可得EF∥AB，EF=AF=AD=x，即可证得△CEF∽△CBA，然后由相似三角形的对应边成比例，求得AD的长，继而求得菱形的周长．
解答 解：设AD=x，
∵四边形ADEF是菱形，
∴EF∥AB，EF=AF=AD=x，
∴△CEF∽△CBA，
∴$\frac{CF}{AC}=\frac{EF}{AB}$，
∵AC=10，AB=15，
∴CF=AC-AF=10-x，
∴$\frac{10-x}{10}=\frac{x}{15}$，
解得：x=6，
∴AD=6，
∴菱形的周长是：24．
故选C．
点评 此题考查了菱形的性质以及相似三角形的判定与性质．注意证得△CEF∽△CBA，根据相似三角形的对应边成比例，利用方程思想求解．
练习册系列答案
课课优能力培优100分系列答案
优百分课时互动系列答案
相关题目
4．下列各式中能用平方差公式计算的是（ ）
| A． | （a+b）（b+a） | B． | （-a+b）（a-b） | C． | （$\frac{1}{3}$a+b）（b-$\frac{1}{3}$a） | D． | （a2-b）（b2+a） |
5．
如图，在8×4的矩形网格中，每格小正方形的边长都是1，若△ABC的三个顶点在图中相应的格点上，图中点D、点E、点F也都在格点上，则下列与△ABC相似的三角形是（ ）
如图，在8×4的矩形网格中，每格小正方形的边长都是1，若△ABC的三个顶点在图中相应的格点上，图中点D、点E、点F也都在格点上，则下列与△ABC相似的三角形是（ ）| A． | △ACD | B． | △ADF | C． | △BDF | D． | △CDE |
6．
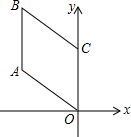如图，四边形OABC是菱形，若OA=2，∠AOC=45°，则B点的坐标是 （ ）
如图，四边形OABC是菱形，若OA=2，∠AOC=45°，则B点的坐标是 （ ）| A． | （-2，2+$\sqrt{2}$） | B． | （2，2+$\sqrt{2}$） | C． | （$-\sqrt{2}$，2+$\sqrt{2}$） | D． | （$\sqrt{2}$，2+$\sqrt{2}$） |
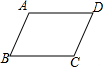如图所示，四边形ABCD是平行四边形．
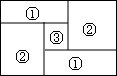如图，小明家的住房平面图呈长方形，被分割成3个正方形和2个长方形后仍是中心对称图形．若只知道原住房平面图长方形的周长，则分割后不用测量就能知道周长的图形的标号为（ ）