题目内容
20．解下列分式方程：（1）$\frac{x}{x-2}$-$\frac{1-{x}^{2}}{（x-2）（x-3）}$=$\frac{2x}{x-3}$；
（2）$\frac{x+1}{x-1}$-$\frac{4}{{x}^{2}-1}$=1．
分析 （1）先把方程两边同时乘以（x-2）（x-3），求出x的值，代入公分母进行检验即可；
（2）先把方程两边同时乘以（x+1）（x-1），求出x的值，代入公分母进行检验即可．
解答 解：（1）方程两边同时乘以（x-2）（x-3）得，x（x-3）-（1-x2）=2x（x-2），解得x=1，
检验：当x=1时，（x-2）（x-3）=（1-2）（1-3）=2≠0，
故x=1是原分式方程的解；
（2）方程两边同时乘以（x+1）（x-1）得，（x+1）2-4=x2-1，解得x=1，
检验：当x=1时，（x+1）（x-1）=（1+1）（1-1）=0，
故x=1是原分式方程的增根，原分式方程无解．
点评 本题考查的是解分式方程，在解答此类问题时要注意验根．
练习册系列答案
相关题目
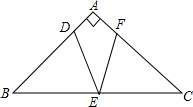如图，△ABC是等腰直角三角形，∠A=90°，点D为AB边上一点，E为BC的中点，将线段DE绕点E顺时针旋转45°后与AC交于点F．
