题目内容
16.已知关于x的方程x2-3x+2-m2=0(1)当m=0时,解这个方程;
(2)若x=4是这个方程的一个根,求m的值及这个方程的另一个根;
(3)无论m取何值,这个方程是否总有两个不相等的实数根?请说明理由.
分析 (1)将m=0代入原方程得出x2-3x+2=0,利用分解因式法解方程即可;
(2)将x=4代入原方程得出关于m的一元二次方程,求出m的值,再将m2的值代入原方程得出x2-3x-4=0,利用分解因式法解方程即可得出结论;
(3)由根的判别式b2-4ac≥1,可以得知方程总有两个不相等的实数根.
解答 解:(1)当m=0时,原方程为x2-3x+2=0,
即(x-1)(x-2)=0,
解得:x1=1,x2=2.
(2)将x=4代入原方程得:
42-3×4+2-m2=0,即m2=6,
∴m1=-$\sqrt{6}$,m2=$\sqrt{6}$.
将m2=6代入原方程得:x2-3x-4=0,
即(x+1)(x-4)=0,
解得:x1=-1,x2=4.
答:若x=4是这个方程的一个根,m的值为±$\sqrt{6}$,这个方程的另一个根为-1.
(3)∵△=b2-4ac=(-3)2-4×(2-m2)=4m2+1≥1,
∴无论m取何值,这个方程总有两个不相等的实数根.
点评 本题考查了根的判别式以及分解因式法解方程,解题的关键是:(1)利用分解因式法解方程;(2)代入x=4求m的值;(3)利用根的判别式b2-4ac恒大于0得出结论.本题属于基础题,难度不大,解决该题型题目时,由根的判别式断定实数根的个数很关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.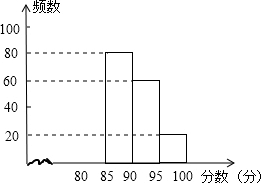 某校组织了“安全在我心中”知识竞赛活动.根据获奖同学在竞赛中的成绩制成的统计图表如下:
某校组织了“安全在我心中”知识竞赛活动.根据获奖同学在竞赛中的成绩制成的统计图表如下:
根据以上图表提供的信息,解答下列问题:
(1)求出表中a、b、c的数值,并补全频数分布直方图;
(2)如果成绩在95分以上(含95分)的可以获得特等奖,那么获奖的同学获得特等奖的概率是多少?
(3)获奖成绩的中位数落在哪个分数段?并估算全部获奖同学的平均分.
 某校组织了“安全在我心中”知识竞赛活动.根据获奖同学在竞赛中的成绩制成的统计图表如下:
某校组织了“安全在我心中”知识竞赛活动.根据获奖同学在竞赛中的成绩制成的统计图表如下:| 分数段 | 频数 | 频率 |
| 80≤x<85 | a | 0.2 |
| 85≤x<90 | 80 | b |
| 90≤x<95 | 60 | c |
| 95≤x<100 | 20 | 0.1 |
(1)求出表中a、b、c的数值,并补全频数分布直方图;
(2)如果成绩在95分以上(含95分)的可以获得特等奖,那么获奖的同学获得特等奖的概率是多少?
(3)获奖成绩的中位数落在哪个分数段?并估算全部获奖同学的平均分.
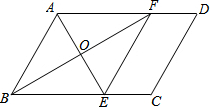 如图,在?ABCD中,∠BAD的平分线交BC于点E,∠ABC的平分线交AD于点F,AE与BF相交于点O,连接EF.
如图,在?ABCD中,∠BAD的平分线交BC于点E,∠ABC的平分线交AD于点F,AE与BF相交于点O,连接EF.
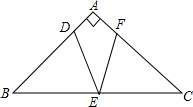 如图,△ABC是等腰直角三角形,∠A=90°,点D为AB边上一点,E为BC的中点,将线段DE绕点E顺时针旋转45°后与AC交于点F.
如图,△ABC是等腰直角三角形,∠A=90°,点D为AB边上一点,E为BC的中点,将线段DE绕点E顺时针旋转45°后与AC交于点F.