题目内容
19.计算:(1)($\frac{1}{3}$)-1+($\frac{1}{2}$)2×(-2)3-(π-3)0.
(2)4xy2•(-$\frac{3}{8}$x2yz3).
分析 (1)本题涉及零指数幂、负整数指数幂等考点.在计算时,需要针对每个考点分别进行计算,然后根据实数的运算法则求得计算结果;
(2)根据单项式的乘法法则,同底数幂的乘法的性质计算即可.
解答 解:(1)原式=$\frac{1}{\frac{1}{3}}$-2-1
=3-2-1
=0;
(2)4xy2•(-$\frac{3}{8}$x2yz3)=4×(-$\frac{3}{8}$)(x•x2)(y2•y)z3=-$\frac{3}{2}$x3y3z3.
点评 本题考查实数的综合运算能力和单项式乘单项式,解决此类题目的关键是熟练掌握零指数幂、负指数幂等考点的运算.

练习册系列答案
相关题目
4.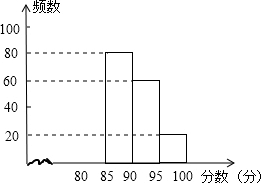 某校组织了“安全在我心中”知识竞赛活动.根据获奖同学在竞赛中的成绩制成的统计图表如下:
某校组织了“安全在我心中”知识竞赛活动.根据获奖同学在竞赛中的成绩制成的统计图表如下:
根据以上图表提供的信息,解答下列问题:
(1)求出表中a、b、c的数值,并补全频数分布直方图;
(2)如果成绩在95分以上(含95分)的可以获得特等奖,那么获奖的同学获得特等奖的概率是多少?
(3)获奖成绩的中位数落在哪个分数段?并估算全部获奖同学的平均分.
 某校组织了“安全在我心中”知识竞赛活动.根据获奖同学在竞赛中的成绩制成的统计图表如下:
某校组织了“安全在我心中”知识竞赛活动.根据获奖同学在竞赛中的成绩制成的统计图表如下:| 分数段 | 频数 | 频率 |
| 80≤x<85 | a | 0.2 |
| 85≤x<90 | 80 | b |
| 90≤x<95 | 60 | c |
| 95≤x<100 | 20 | 0.1 |
(1)求出表中a、b、c的数值,并补全频数分布直方图;
(2)如果成绩在95分以上(含95分)的可以获得特等奖,那么获奖的同学获得特等奖的概率是多少?
(3)获奖成绩的中位数落在哪个分数段?并估算全部获奖同学的平均分.
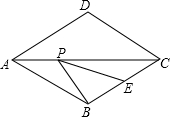 如图,菱形ABCD的边长为4,∠DAB=60°,E为BC的中点,在对角线AC上存在一点P,使△PBE的周长最小,则△PBE的周长的最小值为2$\sqrt{3}$+2.
如图,菱形ABCD的边长为4,∠DAB=60°,E为BC的中点,在对角线AC上存在一点P,使△PBE的周长最小,则△PBE的周长的最小值为2$\sqrt{3}$+2.
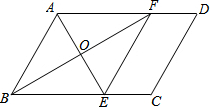 如图,在?ABCD中,∠BAD的平分线交BC于点E,∠ABC的平分线交AD于点F,AE与BF相交于点O,连接EF.
如图,在?ABCD中,∠BAD的平分线交BC于点E,∠ABC的平分线交AD于点F,AE与BF相交于点O,连接EF.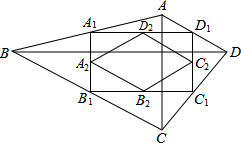 如图,四边形ABCD中,AC=a,BD=b,且AC⊥BD,顺次连接四边形ABCD各边中点,得到四边形A1B1C1D1,再顺次连接四边形A1B1C1D1各边中点,得到四边形A2B2C2D2,如此进行下去,得到四边形AnBnCnDn.
如图,四边形ABCD中,AC=a,BD=b,且AC⊥BD,顺次连接四边形ABCD各边中点,得到四边形A1B1C1D1,再顺次连接四边形A1B1C1D1各边中点,得到四边形A2B2C2D2,如此进行下去,得到四边形AnBnCnDn.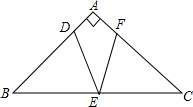 如图,△ABC是等腰直角三角形,∠A=90°,点D为AB边上一点,E为BC的中点,将线段DE绕点E顺时针旋转45°后与AC交于点F.
如图,△ABC是等腰直角三角形,∠A=90°,点D为AB边上一点,E为BC的中点,将线段DE绕点E顺时针旋转45°后与AC交于点F.