题目内容
3．若不论x取何实数，分式$\frac{2x-3}{{x}^{2}+4x+m}$总有意义，求m的取值范围．分析 先读懂题意，知分式有意义的条件是分母永远不为0，得出方程x2+4x+m=0，求出方程无解的条件即可．
解答 解：设x2+4x+m=0，
△=b2-4ac=42-4×1×m=16-4m＜0，
m＞4，
即当m＞4时，方程x2+4x+m=0无解，
即此时不论x取何实数，分式$\frac{2x-3}{{x}^{2}+4x+m}$总有意义，
所以m的取值范围是m＞4．
点评 本题考查了分式有意义的条件和根的判别式的应用，能读懂题意是解此题的关键．
练习册系列答案
相关题目
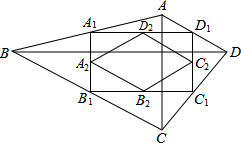如图，四边形ABCD中，AC=a，BD=b，且AC⊥BD，顺次连接四边形ABCD各边中点，得到四边形A1B1C1D1，再顺次连接四边形A1B1C1D1各边中点，得到四边形A2B2C2D2，如此进行下去，得到四边形AnBnCnDn．
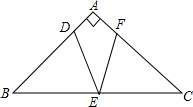如图，△ABC是等腰直角三角形，∠A=90°，点D为AB边上一点，E为BC的中点，将线段DE绕点E顺时针旋转45°后与AC交于点F．