题目内容
17.解分式方程:$\frac{1}{x+10}$$+\frac{1}{(x+1)(x+2)}$$+\frac{1}{(x+2)(x+3)}$+…+$\frac{1}{(x+9)(x+10)}$=2.分析 将方程左边依据$\frac{1}{n(n+1)}=\frac{1}{n}-\frac{1}{n+1}$展开后化简成$\frac{1}{x+1}$=2,解得x的值.
解答 解:由原方程可得:$\frac{1}{x+10}$+$\frac{1}{x+1}$-$\frac{1}{x+2}$+$\frac{1}{x+2}$-$\frac{1}{x+3}$+…+$\frac{1}{x+9}$-$\frac{1}{x+10}$=2,
即:$\frac{1}{x+1}$=2,
去分母,得:2(x+1)=1,
解得:x=-$\frac{1}{2}$,
经检验:x=-$\frac{1}{2}$是原方程的解,
故原分式方程的解为:x=-$\frac{1}{2}$.
点评 本题主要考查解分式方程的能力,依据$\frac{1}{n(n+1)}=\frac{1}{n}-\frac{1}{n+1}$化简原分式方程是解题的关键.

练习册系列答案
相关题目
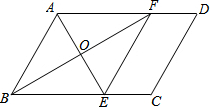 如图,在?ABCD中,∠BAD的平分线交BC于点E,∠ABC的平分线交AD于点F,AE与BF相交于点O,连接EF.
如图,在?ABCD中,∠BAD的平分线交BC于点E,∠ABC的平分线交AD于点F,AE与BF相交于点O,连接EF.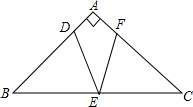 如图,△ABC是等腰直角三角形,∠A=90°,点D为AB边上一点,E为BC的中点,将线段DE绕点E顺时针旋转45°后与AC交于点F.
如图,△ABC是等腰直角三角形,∠A=90°,点D为AB边上一点,E为BC的中点,将线段DE绕点E顺时针旋转45°后与AC交于点F.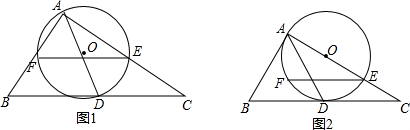

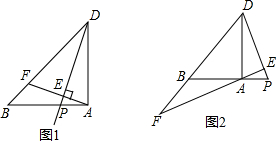 △ABD中,AB=AD,∠BAD=90°,P为直线AB上一动点,AE⊥DP于E,交直线BD于F.
△ABD中,AB=AD,∠BAD=90°,P为直线AB上一动点,AE⊥DP于E,交直线BD于F.