题目内容
6.如图1,在等腰Rt△ABC中,AC=BC,D为边BC上一动点,过B作BE⊥AD于E,过D作DF⊥AB于F.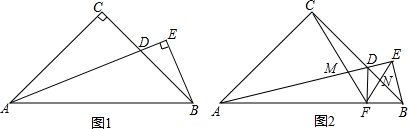
(1)当∠CAD=∠BAD时,求证:AD=2BE;
(2)如图2,当D在边BC上运动时,AD交CF于M,BD与EF交于N,求证:tan∠BAD=$\frac{DM•NB}{DN•MA}$.
分析 (1)连接CE,由等腰三角形的性质得出∠BAC=∠ABC=45°,证明A、B、E、C四点共圆,由圆周角定理得出$\widehat{CE}=\widehat{BE}$,由圆心角、弧、弦之间的关系得出CE=BE,由圆周角定理得出∠AEC=∠ABC=45°,取AD的中点G,连接CG,由直角三角形斜边上的中线性质得出CG=$\frac{1}{2}$AD=CG,由等腰三角形的性质得出∠ACG=∠CAD=22.5°,由三角形的外角性质证出∠CGE=∠AEC,得出CG=CE,因此CG=BE,即可得出AD=2BE;
(2)过点D作PQ∥AB,交CF于点P,交EF于点Q;证明A、C、D、F四点共圆,由圆周角定理得出∠CFD=∠DAC,同理可证∠EFD=∠DBE=∠DAF,证出∠PFD=∠QFD,得出tan∠PFD=tan∠QFD,因此$\frac{PD}{FD}$=$\frac{QD}{FD}$,得出PD=QD;证出△BDF为等腰直角三角形,DF=BF;证明△DPM∽△AFM,得出$\frac{DM}{MA}$=$\frac{DP}{AF}$;同理可证:$\frac{DN}{NB}$=$\frac{DQ}{BF}$=$\frac{DQ}{DF}$,得出$\frac{DM}{MA}•\frac{NB}{DN}$=$\frac{DF}{AF}$,即可得出结论.
解答 (1)证明:连接CE,如图1所示: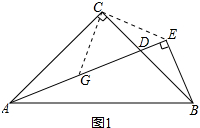
∵等腰Rt△ABC中,AC=BC,
∴∠BAC=∠ABC=45°,
∵BE⊥AD,
∴∠AEB=90°=∠ACB,
∴A、B、E、C四点共圆,
∵∠CAD=∠BAD,
∴∠CAD=∠BAD=$\frac{1}{2}$∠BAC=22.5°,$\widehat{CE}=\widehat{BE}$,
∴CE=BE,∠AEC=∠ABC=45°,
取AD的中点G,连接CG,
∴CG=$\frac{1}{2}$AD=CG,
∴∠ACG=∠CAD=22.5°,
∴∠CGE=∠CAD+∠ACG=45°=∠AEC,
∴CG=CE,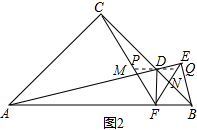
∴CG=BE,
∴AD=2BE;
(2)证明:过点D作PQ∥AB,交CF于点P,交EF于点Q;如图2所示:
∵DF⊥AB,∠ACD=90°,
∴∠ACD+∠AFD=180°,
∴A、C、D、F四点共圆,
∴∠CFD=∠DAC,同理可证∠EFD=∠DBE=∠DAF,而∠CAD=∠EBD,
∴∠PFD=∠QFD,
∴tan∠PFD=tan∠QFD,
即$\frac{PD}{FD}$=$\frac{QD}{FD}$,
∴PD=QD;由∠DBF=45°,DF⊥BF知:
△BDF为等腰直角三角形,DF=BF;
∵DP∥AF,
∴△DPM∽△AFM,
∴$\frac{DM}{MA}$=$\frac{DP}{AF}$;
同理可证:$\frac{DN}{NB}$=$\frac{DQ}{BF}$=$\frac{DQ}{DF}$,
∴$\frac{DM}{MA}•\frac{NB}{DN}$=$\frac{DF}{AF}$,
∵tan∠BAD=tan∠DAF=$\frac{DF}{AF}$,
∴tan∠BAD=$\frac{DM•NB}{DN•MA}$.
点评 本题是四边形综合题目,考查了等腰直角三角形的性质、四点共圆、圆周角定理、直角三角形斜边上的中线性质、相似三角形的判定与性质等知识;证明四点共圆,运用圆周角定理得出相等的角和相等的弧是解决问题的突破口.

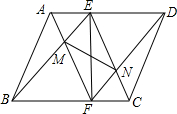 如图,在?ABCD中,点E在AD上,连BE,DF∥BE交BC于点F,AF与BE交于点M,CE与DF交于点N.求证:EF与MN互相平分.
如图,在?ABCD中,点E在AD上,连BE,DF∥BE交BC于点F,AF与BE交于点M,CE与DF交于点N.求证:EF与MN互相平分. 如图,在⊙O中,P为$\widehat{BAC}$的中点,PD⊥CD,CD交⊙O于A,若AC=3,AD=2,则AB的长为7.
如图,在⊙O中,P为$\widehat{BAC}$的中点,PD⊥CD,CD交⊙O于A,若AC=3,AD=2,则AB的长为7. 如图是两块完全一样的含30°角的三角板,分别记作△ABC和△A1B1C1,现将两块三角板重叠在一起,高较长直角边的中点为M,绕中点M转动上面的三角板ABC,直角顶点C恰好落在三角板△A1B1C1的斜边A1B1上.当∠A=30°,B1C=2时,则此时AB的长为( )
如图是两块完全一样的含30°角的三角板,分别记作△ABC和△A1B1C1,现将两块三角板重叠在一起,高较长直角边的中点为M,绕中点M转动上面的三角板ABC,直角顶点C恰好落在三角板△A1B1C1的斜边A1B1上.当∠A=30°,B1C=2时,则此时AB的长为( )