题目内容
10．
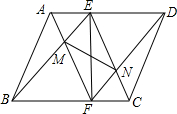如图，在?ABCD中，点E在AD上，连BE，DF∥BE交BC于点F，AF与BE交于点M，CE与DF交于点N．求证：EF与MN互相平分．
分析 由在?ABCD中，DF∥BE，易证得四边形BEDF是平行四边形，即可证得AE=CF，继而证得四边形AFCE是平行四边形，进而证得四边形EMFN是平行四边形，则可证得结论．
解答 证明：∵四边形ABCD是平行四边形，
∴AD∥BC，AD=BC，
∵DF∥BE，
∴四边形BEDF是平行四边形，
∴DE=BF，
∴AE=CF，
∴四边形AFCE是平行四边形，
∴AF∥CE，
∴四边形EMFN是平行四边形，
∴EF与MN互相平分．
点评 此题考查了平行四边形的判定与性质．注意证得四边形EMFN是平行四边形是关键．
练习册系列答案
相关题目
如图，在四边形ABCD中，AO是∠DAB的平分线，BO是∠ABC的平分线，AO与BO交于点O．若∠C+∠D=120°，求∠AOB的度数．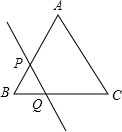
如图，在正△ABC中，AB=10cm，直线PQ由点B出发，沿BA的方向匀速运动，速度为1cm/s，运动时间为t（s）（0＜t＜5），则BP=$\frac{2\sqrt{3}}{3}t$．（用t的代数式表示）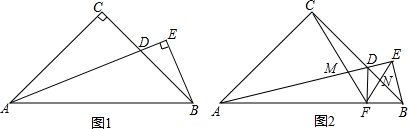
2．若长方形的一边长为3m+n，另一边比它长m-n（m＞n），则这个长方形的面积是（ ）
| A． | 12m2+4mn | B． | 12m2-4mn | C． | 3m2-2mn-n2 | D． | 3m2+2mn-n2 |
如图，在△ABC中，DE∥BC，DF∥AB，D，E，M分别为AC，AB，BE的中点，连接DM，以DM为边作△DMN，连接FN，且DM=DN．若∠B=∠C=∠MDN=60°，AB=6，则FN的长度为$\frac{3}{2}$．