题目内容
1. 如图,在⊙O中,P为$\widehat{BAC}$的中点,PD⊥CD,CD交⊙O于A,若AC=3,AD=2,则AB的长为7.
如图,在⊙O中,P为$\widehat{BAC}$的中点,PD⊥CD,CD交⊙O于A,若AC=3,AD=2,则AB的长为7.
分析 连接PC PB PA,过P做BA垂线于H点,根据P为$\widehat{BAC}$的中点可知PB=PC,再由全等三角形的判定定理可得出△PBH≌△PCD,Rt△PHA≌Rt△PDA,根据AC=AD=1即可得出结论.
解答 解:连接PC PB PA,过P做BA垂线于H点
∵P为$\widehat{BAC}$的中点
∴PB=PC
∴∠B=∠C,∠PHB=∠PDA,
∴∠BPH=∠DPC,
在△PBH与△PCD中,
$\left\{\begin{array}{l}{∠B=∠C}\\{PB=PC}\\{∠BPH=∠DPC}\end{array}\right.$,
∴△PBH≌△PCD(ASA),
∴BH=CD=5,PH=PD,
在Rt△PHA与Rt△PDA中,
$\left\{\begin{array}{l}{PH=PD}\\{=A=PA}\end{array}\right.$,
∴Rt△PHA≌Rt△PDA(HL),
∴HA=AD=2,
∴AB=BH+HA=7.
故答案为:7.
点评 本题考查的是圆周角定理及全等三角形的判定与性质,根据题意作出辅助线,构造出全等三角形是解答此题的关键.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
2.若长方形的一边长为3m+n,另一边比它长m-n(m>n),则这个长方形的面积是( )
| A. | 12m2+4mn | B. | 12m2-4mn | C. | 3m2-2mn-n2 | D. | 3m2+2mn-n2 |
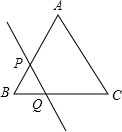 如图,在正△ABC中,AB=10cm,直线PQ由点B出发,沿BA的方向匀速运动,速度为1cm/s,运动时间为t(s)(0<t<5),则BP=$\frac{2\sqrt{3}}{3}t$.(用t的代数式表示)
如图,在正△ABC中,AB=10cm,直线PQ由点B出发,沿BA的方向匀速运动,速度为1cm/s,运动时间为t(s)(0<t<5),则BP=$\frac{2\sqrt{3}}{3}t$.(用t的代数式表示)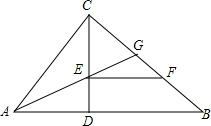 如图,△ABC中,∠ACB=90°,CD是高,AG平分∠CAB,EF∥AB,AC=6,BC=8.
如图,△ABC中,∠ACB=90°,CD是高,AG平分∠CAB,EF∥AB,AC=6,BC=8.
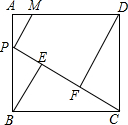 如图,P为正方形ABCD的边AB上的一个动点(点P不与A、B重合),连结PC,作BE⊥PC,DF⊥PC,垂足分别为点E、F,已知AD=5.
如图,P为正方形ABCD的边AB上的一个动点(点P不与A、B重合),连结PC,作BE⊥PC,DF⊥PC,垂足分别为点E、F,已知AD=5. 如图,在平面直角坐标系中,四边形OABC是边长为8的正方形,M(8,m)、N(n,8)分别是线段AB、BC上的两个动点,且ON⊥MN,当OM最小时,m+n=10.
如图,在平面直角坐标系中,四边形OABC是边长为8的正方形,M(8,m)、N(n,8)分别是线段AB、BC上的两个动点,且ON⊥MN,当OM最小时,m+n=10.