题目内容
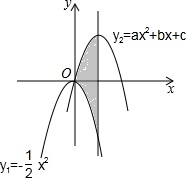 把y1=-
把y1=-| 1 |
| 2 |
(1)求图中阴影部分面积;
(2)求平移后的图象对应的函数关系式;
(3)求使y1随x增大而减少且y2随x增大而增大的x的范围.
考点:二次函数图象与几何变换
专题:
分析:(1)根据原抛物线的顶点坐标,由平移规律进而求得新抛物线的解析式,把(0,0)代入即可得到新抛物线解析式,阴影部分的面积等于三角形的面积,再根据三角形的面积公式列式计算即可得解.
(2)根据(1)的解题过程可以得到新抛物线的解析式;
(3)根据图示可以直接得到答案.
(2)根据(1)的解题过程可以得到新抛物线的解析式;
(3)根据图示可以直接得到答案.
解答:
 解:(1)设平移后抛物线的解析式为y=-
解:(1)设平移后抛物线的解析式为y=-
(x-1)2+b.
把(0,0)代入得到:0=-
(0-1)2+b,
解得 b=
.
则平移后抛物线的顶点坐标是(1,
).
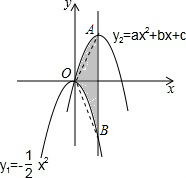
如图,连接OA、OB.则图中阴影部分的面积=
×2×
×1=
;
(2)由(1)易得新抛物线的解析式为:y=-
(x-1)2+
=-
x2-x+1.
(3)由图示知,当0<x<1时,y1随x增大而减少且y2随x增大而增大.
 解:(1)设平移后抛物线的解析式为y=-
解:(1)设平移后抛物线的解析式为y=-| 1 |
| 2 |
把(0,0)代入得到:0=-
| 1 |
| 2 |
解得 b=
| 1 |
| 2 |
则平移后抛物线的顶点坐标是(1,
| 1 |
| 2 |
如图,连接OA、OB.则图中阴影部分的面积=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(2)由(1)易得新抛物线的解析式为:y=-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(3)由图示知,当0<x<1时,y1随x增大而减少且y2随x增大而增大.
点评:本题考查了二次函数图象与几何变换.讨论两个二次函数的图象的平移问题,只需看顶点坐标是如何平移得到的即可.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目
下列方程变形错误的是( )
A、由方程
| ||||
B、由方程
| ||||
C、由方程
| ||||
D、由方程x-
|
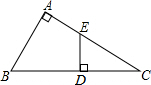 如图,已知∠A=90°,AB=BD,ED⊥BC于D.求证:AE=ED.
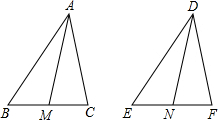
如图,已知∠A=90°,AB=BD,ED⊥BC于D.求证:AE=ED.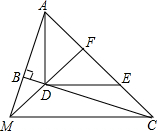 如图,∠ABC=90°,D、E分别在BC、AC上,AD⊥DE,且AD⊥DE,点F是AE的中点,FD与AB的延长线相交于点M,连结MC.
如图,∠ABC=90°,D、E分别在BC、AC上,AD⊥DE,且AD⊥DE,点F是AE的中点,FD与AB的延长线相交于点M,连结MC.