题目内容
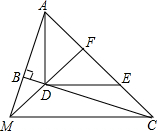 如图,∠ABC=90°,D、E分别在BC、AC上,AD⊥DE,且AD⊥DE,点F是AE的中点,FD与AB的延长线相交于点M,连结MC.
如图,∠ABC=90°,D、E分别在BC、AC上,AD⊥DE,且AD⊥DE,点F是AE的中点,FD与AB的延长线相交于点M,连结MC.(1)求证:∠FMC=∠FCM;
(2)AD与MC垂直吗?请说明理由.
考点:全等三角形的判定与性质
专题:
分析:(1)根据等腰直角三角形的性质得出DF⊥AE,DF=AF=EF,再证明△DFC≌△AFM,得出FC=FM,即可证出结论;
(2)由(1)得:∠DFC=90°,DF=EF,∠FDE=∠FMC=45°,再证明DE∥MC,即可得出结论.
(2)由(1)得:∠DFC=90°,DF=EF,∠FDE=∠FMC=45°,再证明DE∥MC,即可得出结论.
解答:
解:(1)证明:∵△ADE是等腰直角三角形,F是AE的中点,
∴DF⊥AE,DF=AF=EF,
∴∠AFM=90°,
∴∠FAM+∠AMF=90°,
∵∠ABC=90°,
∴∠FAM+∠DCF=90°,
∴∠DCF=∠AMF,
在△DFC和△AFM中,
,
∴△DFC≌△AFM(AAS),
∴FC=FM,
∴∠FMC=∠FCM;
(2)AD⊥MC;理由如下:
由(1)得:∠DFC=90°,DF=EF,FM=FC,
∴∠FDE=∠FMC=45°,
∴DE∥MC,
∵AD⊥DE,
∴AD⊥MC.
∴DF⊥AE,DF=AF=EF,
∴∠AFM=90°,
∴∠FAM+∠AMF=90°,
∵∠ABC=90°,
∴∠FAM+∠DCF=90°,
∴∠DCF=∠AMF,
在△DFC和△AFM中,
|
∴△DFC≌△AFM(AAS),
∴FC=FM,
∴∠FMC=∠FCM;
(2)AD⊥MC;理由如下:
由(1)得:∠DFC=90°,DF=EF,FM=FC,
∴∠FDE=∠FMC=45°,
∴DE∥MC,
∵AD⊥DE,
∴AD⊥MC.
点评:本题考查了等腰直角三角形的性质与判定以及全等三角形的判定与性质;熟练掌握全等三角形的判定方法,证明三角形全等是解决问题的关键.

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
△ABC中有六个元素,只要已知其中的某些元素就可以作出这个三角形,根据以下给出的条件,可作出△ABC的有( )个.
①已知三边;②已知两边及其夹角;③已知两角及其夹边;④已知两角和其中一角的对边.
①已知三边;②已知两边及其夹角;③已知两角及其夹边;④已知两角和其中一角的对边.
| A、1 | B、2 | C、3 | D、4 |
二次函数y=x2-2x+m与x轴有交点,则m应满足的条件是( )
| A、m>1 | B、m≥1 |
| C、m<1 | D、m≤1 |
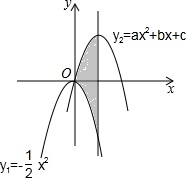 把y1=-
把y1=-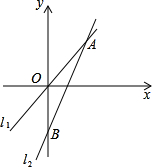 如图,已知:A(3,4),|OB|=2|OA|,求出直线l1和l2的解析式.
如图,已知:A(3,4),|OB|=2|OA|,求出直线l1和l2的解析式.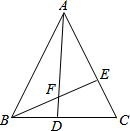 边长为4的等边△ABC,D,E分别在BC,AC上移动,D点从B运动到C,E从C运动到A.已知:D,E同时同速移动,连AD、BE交于F.
边长为4的等边△ABC,D,E分别在BC,AC上移动,D点从B运动到C,E从C运动到A.已知:D,E同时同速移动,连AD、BE交于F.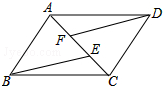 如图,已知点A、F、E、C在同一直线上,AB∥CD,∠ABE=∠CDF,AF=CE.
如图,已知点A、F、E、C在同一直线上,AB∥CD,∠ABE=∠CDF,AF=CE.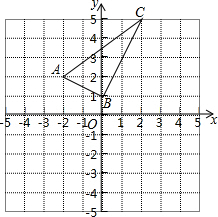 如图,直角坐标系中的网格由单位正方形组成,三角形ABC中,C点坐标为(2,5).
如图,直角坐标系中的网格由单位正方形组成,三角形ABC中,C点坐标为(2,5).