题目内容
用适当的方法解方程.
(1)x2+3x-2=0
(2)x2-6x+9=(5-2x)2.
(1)x2+3x-2=0
(2)x2-6x+9=(5-2x)2.
考点:解一元二次方程-因式分解法,解一元二次方程-公式法
专题:
分析:(1)先找出a=1,b=3,c=-2,再利用公式法求出方程的解;
(2)先把x2-6x+9=(5-2x)2转化为(x-3)2-(5-2x)2=0,然后因式分解得到(-x+2)(3x-8)=0,解两个一元一次方程即可.
(2)先把x2-6x+9=(5-2x)2转化为(x-3)2-(5-2x)2=0,然后因式分解得到(-x+2)(3x-8)=0,解两个一元一次方程即可.
解答:
解:(1)∵x2+3x-2=0,
∴a=1,b=3,c=-2,
∴△=b2-4ac=32-4×1×(-2)=17>0,
∴x=
=
,
∴x1=
,x2=
.
(2)∵x2-6x+9=(5-2x)2,
∴(x-3)2=(5-2x)2,
∴(x-3)2-(5-2x)2=0,
∴[(x-3)+(5-2x)][(x-3)-(5-2x)]=0,
∴(x-3+5-2x)(x-3-5+2x)=0,
∴(-x+2)(3x-8)=0,
∴(-x+2)=0或(3x-8)=0,
∴x1=2,x2=
.
∴a=1,b=3,c=-2,
∴△=b2-4ac=32-4×1×(-2)=17>0,
∴x=
-b±
| ||
| 2a |
-3±
| ||
| 2 |
∴x1=
-3+
| ||
| 2 |
-3-
| ||
| 2 |
(2)∵x2-6x+9=(5-2x)2,
∴(x-3)2=(5-2x)2,
∴(x-3)2-(5-2x)2=0,
∴[(x-3)+(5-2x)][(x-3)-(5-2x)]=0,
∴(x-3+5-2x)(x-3-5+2x)=0,
∴(-x+2)(3x-8)=0,
∴(-x+2)=0或(3x-8)=0,
∴x1=2,x2=
| 8 |
| 3 |
点评:本题主要考查了因式分解法和公式法解一元二次方程的知识,解答本题的关键是熟练掌握解因式分解法和公式法解一元二次方程的基本步骤,此题难度不大.

练习册系列答案
相关题目
二次函数y=x2-2x+m与x轴有交点,则m应满足的条件是( )
| A、m>1 | B、m≥1 |
| C、m<1 | D、m≤1 |
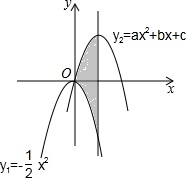 把y1=-
把y1=-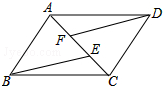 如图,已知点A、F、E、C在同一直线上,AB∥CD,∠ABE=∠CDF,AF=CE.
如图,已知点A、F、E、C在同一直线上,AB∥CD,∠ABE=∠CDF,AF=CE. 如图,△ABC中,CD⊥AB于D,若AD=2BD,AC=6,BC=
如图,△ABC中,CD⊥AB于D,若AD=2BD,AC=6,BC= 如图,已知AD垂直平分BC,∠ABC的平分线交AD于点O,连接OC.若∠AOC=120°,BC长为2
如图,已知AD垂直平分BC,∠ABC的平分线交AD于点O,连接OC.若∠AOC=120°,BC长为2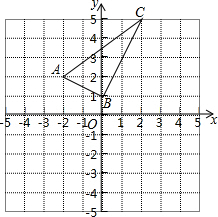 如图,直角坐标系中的网格由单位正方形组成,三角形ABC中,C点坐标为(2,5).
如图,直角坐标系中的网格由单位正方形组成,三角形ABC中,C点坐标为(2,5).