题目内容
矩形的对角线的夹角为120°,两对角线与两短边之和为36,则对角线的长是 ,该矩形的面积是 .
考点:矩形的性质
专题:
分析:先证明△AOB是等边三角形,求出AB=OA=OB=
AC,再由已知条件求出AB、AC,根据勾股定理求出BC,即可求出面积.
| 1 |
| 2 |
解答:
解:如图所示:

∵四边形ABCD是矩形,
∴AC=BD,OA=
AC,OB=
BD,∠ABC=90°,AB=CD,
∴OA=OB,
∵∠AOD=120°,
∴∠AOB=60°,
∴△AOB是等边三角形,
∴AB=OA=OB=
AC,
∵AB+CD+AC+BD=36,
∴6AB=36,
∴AB=6,AC=12,
∴BC=
=6
,
∴矩形的面积=AB•BC=6×6
=36
;
故答案为:12,36
.


∵四边形ABCD是矩形,
∴AC=BD,OA=
| 1 |
| 2 |
| 1 |
| 2 |
∴OA=OB,
∵∠AOD=120°,
∴∠AOB=60°,
∴△AOB是等边三角形,
∴AB=OA=OB=
| 1 |
| 2 |
∵AB+CD+AC+BD=36,
∴6AB=36,
∴AB=6,AC=12,
∴BC=
| 122-62 |
| 3 |
∴矩形的面积=AB•BC=6×6
| 3 |
| 3 |
故答案为:12,36
| 3 |
点评:本题考查了矩形的性质、等边三角形的判定与性质以及勾股定理的运用;熟练掌握矩形的性质综合运用定理进行推理和计算是解题的关键

练习册系列答案
 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
下列计算不正确的是( )
A、3
| ||||||||||
B、
| ||||||||||
C、(
| ||||||||||
| D、-13-8=-21 |
二次函数y=x2-2x+m与x轴有交点,则m应满足的条件是( )
| A、m>1 | B、m≥1 |
| C、m<1 | D、m≤1 |
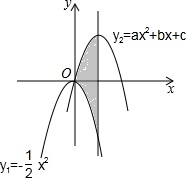 把y1=-
把y1=-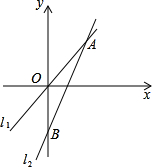 如图,已知:A(3,4),|OB|=2|OA|,求出直线l1和l2的解析式.
如图,已知:A(3,4),|OB|=2|OA|,求出直线l1和l2的解析式.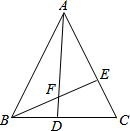 边长为4的等边△ABC,D,E分别在BC,AC上移动,D点从B运动到C,E从C运动到A.已知:D,E同时同速移动,连AD、BE交于F.
边长为4的等边△ABC,D,E分别在BC,AC上移动,D点从B运动到C,E从C运动到A.已知:D,E同时同速移动,连AD、BE交于F.